
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закон Пуассона.
|
|
Пусть СВ Х принимает значения:
Х=0, 1, 2, …, m, …
P(X=m)=Pn(m)=(e-λ λ m)/m!
Р-вероятность появления события А в одном из n независимых испытаний, когда n достаточно велико, а р-мало. λ =nр
Запишем ряд распределения СВ Х, который будет называться законом Пуассона.
| Х | |||
| Р | e-λ | e-λ /1! | e-λ λ 2/2! |
| Х | … | m | … |
| Р | … | e-λ λ m/m! | … |
∞
∑ pі= e-λ + e-λ /1! + e-λ λ 2/2! +...+
і=1
e-λ λ m/m! +...= e-λ (1+λ /1! + λ 2/2! +...+ λ m/m! +…)
Выражение в скобках представдяет собой ряд Маклорена для функции
ex=1+х/1! +х2/2! +…, при х= λ
| 1+ λ /1! + λ 2/2! +…+ λ m/m! |
∞
∑ λ m/m! = eλ
m=0
∑ pі= e-λ * eλ
Определим числовые характеристики закона Пуассона: М(Х)=λ; D(Х)=λ; σ (Х)=√ λ
Доказательства:
∞ ∞
1. М(Х)= ∑ (me-λ λ m)/m! = e-λ ∑ λ m/
m=0 m=1
∞
/(m-1)! = e-λ λ ∑ λ m-1/(m-1)! =e-λ λ * eλ
m=1
=λ
М(Х)=λ, ч.т.д.
2. D(Х)=М(Х2)-(М(Х))2=
∞ ∞
= ∑ (m2e-λ λ m)/m! = e-λ ∑ mλ m/(m-1)! =
m=0 m=1
∞
= ∑ e-λ ∑ ((m-1)+1)λ m/ (m-1)! =
m=1
∞
= e-λ ∑ ((m-1)λ m/(m-1)! +λ m/(m-1)!)=
m=1
∞ ∞
= e-λ ∑ (m-1)λ m/(m-1)! + e-λ ∑ λ m/
m=1 v=1
∞
/(m-1)! = e-λ ∑ λ m-2 λ 2/(m-2)! +
m=2
∞ ∞
+ e-λ ∑ λ m/(m-1)! = e-λ λ 2∑ λ m-2/(m-
m=1 m=2
∞
2)! + e-λ λ ∑ λ m-1/(m-1)! = e-λ λ 2* eλ +
m=1
+ e-λ λ * eλ = λ 2+ λ
М(Х2) = λ 2+ λ
D(Х)=М(Х2)-(М(Х))2= λ 2+ λ - λ 2= λ
D(X)=M(X)= λ
3. σ (Х)=√ D(Х)=√ λ, ч.т.д.
Замечание: закон Пуассона зависит от одного параметра λ; биноминальный закон зависит от n, p.
B(n; p)
31. M(x), D(x) СВ, распределённых по закону Пуассона
M(x)= 
D(x)=M(x2)-(M(x))2
M(x2)= 
D(x)=M(x2)-(M(x))2=  -
-  =
=  (+см. п. 30)
(+см. п. 30)
В законе Пуассона мат. Ожидание равно дисперсии M(x)=D(x)=λ
Закон Пуассона зависит от одного параметра λ, биномиальный закон зависит от n, p
32.)плотность распределения вероятностей непрерывных СВ. Её свойства.
Пусть рассматривается непр. СВ Х ф-ии распр-я F(x), которая непрерывна и диф-на в рассматриваемой области (вся ось OX). Рассмотрим отрезок x+∆ x
P(x< X< x+∆ x)=F(x+∆ x)-F(x)=P(x< X< x+∆ x)/ ∆ x=  ,
,
f(x)=F`(x) (1)плотность распределения вероятностей непр. СВ Х
Вер-ть попадания НСВ на интервал теорема: 
Док-во: P(a< X< b)= F(b)-F(a), где F(x)- ф-я распределения СВ Х.
f(x)=F`(x) - ф-я распр-я F(x) является первообразной для плотности распределения f(x), поэтому  =F(b)-F(a)= =P(a< X< b)
=F(b)-F(a)= =P(a< X< b)
Теорема 2: если известна плотность распределения f(x) НСВ Х, то ф-ия распределения F(x)=  (2)
(2)
Док-во: F(x)=P(X< x)=P(-∞ < X< x)= 
Основные свойства плотности распределения:
1) f(x) определена на (-∞; +∞)
доказательство следует из того, что f(x)=F`(x), а ф-ия распределения F(x) неубывающая, => её производная F`(x)> 0
2) Условия нормировки: 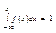 (3) доказательство следует из формулы (2)
(3) доказательство следует из формулы (2)