
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные хар-ки генеральной и выборочной совокупностей.
|
|
Пусть генеральная совокупность имеет распределение

| 
| 
| …. | 
|

| 
| 
| …. | 
|
 -частоты.
-частоты.  -объём генеральной совокупности.
-объём генеральной совокупности.
 -объём выборки. Генеральная средняя
-объём выборки. Генеральная средняя  . Выборочная средняя
. Выборочная средняя 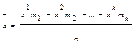 .
.  . Генеральная дисперсия
. Генеральная дисперсия  ,
,  . Выборочная дисперсия
. Выборочная дисперсия  . Генеральная доля(отношение числа объекта e совокупности, обладающей данным признаком к числу всех объектов) -
. Генеральная доля(отношение числа объекта e совокупности, обладающей данным признаком к числу всех объектов) -  . Выборочная доля -
. Выборочная доля -  .
.
46. Оценка параметров распределения. Несмещённость, состоятельность, эффективность оценок. Точечные и интервальные оценки.
Оценкой  параметра
параметра 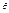 называется любая функция от значений выборки
называется любая функция от значений выборки  , т.е. статистика. Оценка является несмещённой, если
, т.е. статистика. Оценка является несмещённой, если  Если для любого
Если для любого 
 то оценка
то оценка  называется состоятельной. Оценкой качества несмещенной оценки является ее дисперсия. Несмещенная оценка
называется состоятельной. Оценкой качества несмещенной оценки является ее дисперсия. Несмещенная оценка  называется эффективной, если ее дисперсия
называется эффективной, если ее дисперсия  является наименьшей среди дисперсий всех возможных оценок параметра
является наименьшей среди дисперсий всех возможных оценок параметра 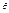 , вычисленных по одному и тому же объему выборки п. Оценки
, вычисленных по одному и тому же объему выборки п. Оценки  называются точечными, так как они оценивают одно численное значение параметра
называются точечными, так как они оценивают одно численное значение параметра 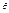 (точку). Точечная оценка
(точку). Точечная оценка  параметра
параметра 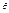 дает лишь некоторое приближенное значение
дает лишь некоторое приближенное значение 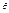 . Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра.
. Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра.
Интервальной оценкой параметра 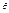 называется интервал (α, β), который с заданной вероятностью γ накрывает неизвестное значение параметра
называется интервал (α, β), который с заданной вероятностью γ накрывает неизвестное значение параметра 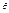 . Такой интервал (α, β) называется доверительным интервалом, а вероятность γ — доверительной вероятностью, или уровнем надежности. Обычно доверительный интервал симметричен относительно оценки
. Такой интервал (α, β) называется доверительным интервалом, а вероятность γ — доверительной вероятностью, или уровнем надежности. Обычно доверительный интервал симметричен относительно оценки  , тогда он определяется формулой
, тогда он определяется формулой 
и имеет вид  т.е. неравенства
т.е. неравенства  выполняется с вероятностью γ. Наибольшее отклонение Δ выборочного значения параметра от его истинного значения называется предельной ошибкой выборки.
выполняется с вероятностью γ. Наибольшее отклонение Δ выборочного значения параметра от его истинного значения называется предельной ошибкой выборки.