Оценка генеральных характеристик по выборке.

Рассмотрим повторную выборку значений гене­ральной совокупности X. При этом случайные величины будут независимыми. Пусть MX= α, DX = δ ² ге­неральные средняя и дисперсия совокупности. В качестве оце­нок для α и δ рассмотрим среднюю арифметическую выборки и выборочную дисперсию .

Выясним свойства этих оценок: 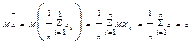. Значит, 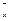является несмещённой оценкой для α. Т.к. по закону больших чисел 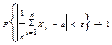при , то оценка является состоятельной. Можно доказать, что оценка 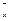является также эффективной, причём . Математическое ожидание выборочной дисперсии равно 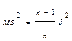. Таким образом, оценка 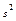является смещённой. На практи­ке, чтобы избавиться от этого недостатка, для оценки неизвест­ной дисперсии генеральной совокупности пользуются исправ­ленной несмещенной оценкой . Тем не менее, из закона больших чисел следует, что как оцен­ка 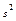, так и 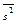являются состоятельными оценками для .Дисперсия , где N -- объем генеральной совокупности. Дисперсия в случае повторной выборки равна 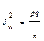, а в случае бесповторной выборки , где .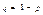

48.Интервальной оценкой параметра называется интервал (a; b), который с заданной вероятностью g накрывает неизвестное значение параметра (интервальная оценка позволяет установить точность и надежность оценок) Интервал(a; b) называется доверительным интервалом (интервал, который покрывает неизвестный параметр с заданной вероятностью g), а вероятность g - доверительной вероятностью

если интервал симметричен относительно оценки : 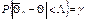он имеет вид 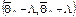. Q* тем точнее определяет параметр Q, чем меньше , т. е.

если d> 0 и < d, то чем меньше d, тем оценка точнее. d(уровень значимости)- характеризует точность оценки.