Доверительный интервал для М(х)в случае нормально распред.ген.совокупности

Пусть CВ Х распределена нормально т. е. ген. с-ть – нормально распределенная CВ с переменными: и . Для нормальной СВ Х с переменными a и s имеет место ф-ла вер-ти отклонения нормальной СВ: .

В нашем случае: , e=D> 0, s(х)= , СВ Х= 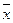. Тогда получаем 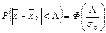. Зададим доверительную вероятность g, тогда . Это вероятность того, что выборочная характеристика отличается от ген средней 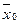по абсолют величине меньше чем на D, тогда имеем: → t_y= 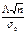. Рассмотрим D= - точность оценки(предельная ош выборки). Получим интервал: на этом интервале с надежностью(доверит вероятностью) g находится неизвестная вероятная средняя Примечание: если s₀ неизвестна, ее заменяют приближенно исправленной стат дисперсией »S

(Если отбор бесповторный, то мера точности D имеет вид: D= )

50.Сред ош в-ки – величина , где - сред квадрат отклонение средней выборки , а - среднее квадрат отклонение ген с-ти; n – объем выборки.(для бесповтор. )

Предел ош вы-ки (D)– наибольшее отклонение выборочной средней от генеральной средней , которое возможно с данной доверительной вероятностью a. D=mt, где m - сред ош в-ки, а t находится из равенства F(t)=a по заданной вероятности a. (используя ф-лу сред.ош. выборки: D= t 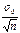)(для бесп. )