Деление целого неотрицательного числа на натуральное.

Рассмотрим задачу, которую решают младшие школьники, приступая к изучению действия деления: «8 апельсинов разложили на тарелки, по 2 апельсина на каждую. Сколько раз по 2 апельсина положили? Сколько тарелок потребовалось?»

Ответ на вопрос задачи находится при помощи деления: 8: 2= 4.

Проанализируем решение этой задачи. В задаче рассматривается множество, в котором 8 элементов. Оно разбивается на подмножества, в каждом из которых по 2 элемента, т. е. на равномощные подмножества.

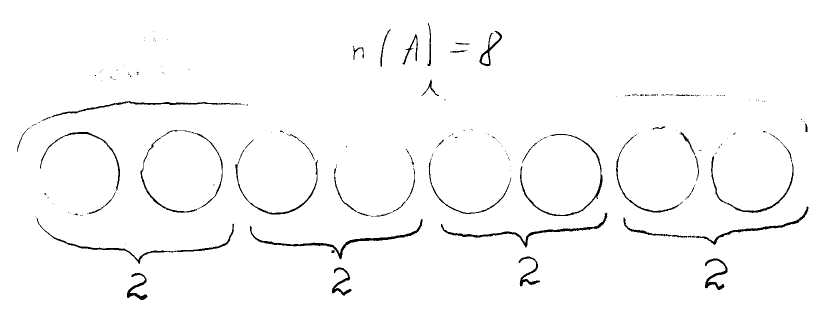
Кроме того, они попарно не пересекаются. В задаче спрашивается, сколько таких подмножеств получилось. Таким образом, число 4, полученное в ответе, - это число двухэлементных подмножеств, на которые разбито множество из 8 элементов.

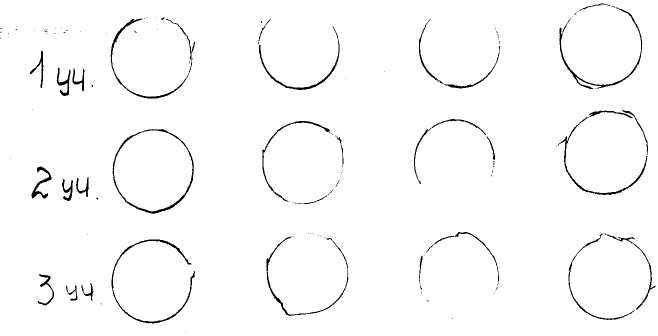
Обратимся теперь к другой задаче: «12 карандашей раздали 3 ученикам поровну. Сколько карандашей получил каждый?»

Она также решается делением: 12: 3= 4 (карандаша). Но число 4 здесь выступает в другом смысле - как число элементов в каждом из трех равномощных непересекающихся подмножеств, на которые разбито множество, содержащее 12 элементов.

В общем виде частное целого неотрицательного числа а и натурального числа б определяется следующим образом: Определение. Пусть а - п (А) и множество А разбито на попарно непересекающиеся равномощные подмножеств

Если б- число элементов каждого подмножества в разбиении множества А, то частным чисел а и б называется число подмножеств в этом разбиении.

Если б - число подмножеств в разбиении множества А, то частным чисел а и б называется число элементов каждого подмножества.

Действие, при помощи которого находят частное чисел а и б, называется делением, число а - делимым, б - делителем.

Виды простых задач на деление

1) деление по содержанию: «12 яблок раздали детям по три каждому. Сколько детей получили яблоки?»

2) деление на равные части: «12 яблок раздали трем детям поровну. Сколько яблок получил каждый ребенок?»

3)нахождение первого множителя по известным произведению и второму множителю: «В трех клетках кроликов было поровну, в каждой по несколько кроликов. Всего в клетках было 12 кроликов. Сколько кроликов было в каждой клетке?»

4)нахождение второго множителя по известным произведению и
первому множителю: «В нескольких клетках сидели кролики, по четыре кролика в каждой клетке. Всего в клетках было 12 кроликов. Сколько было клеток с кроликами?».

5)нахождение делителя по известным частному и делимому: «12 яблок раздали нескольким детям поровну. Каждый ребенок получил по 4 яблока. Сколько детей получили яблоки?»

6)уменьшение числа в несколько раз (прямая форма): «У школы росли 12 берез, а дубов в три раза меньше. Сколько дубов росло у школы?»

7)уменьшение числа в несколько раз (косвенная форма): «У школы росли 12 берез, их в три раза больше, чем дубов. Сколько дубов росло у школы?»

8) кратное сравнение чисел или нахождение отношения двух чисел
(1 вид): «У школы росло 12 берез и 4 дуба. Во сколько раз больше росло берез, чем дубов?»

9) кратное сравнение чисел или нахождение отношения двух чисел

(2 вид): «У школы росло 12 берез и 4 дуба. Во сколько раз меньше росло дубов, чем берез?»