Вопрос 28. Признаки делимости на 2 и 5, на 4 и 25, на 8 и 125, на 3 и 9. Признаки делимости на составные числа.

Признак делимости на:

2: для того, чтобы число х делилось на 2, необходимо и достаточно чтобы его десятичная запись оканчивалась одной из цифр0, 2, 4, 6, 8.

5: для того, чтобы число х делилось на 5, необходимо и достаточно чтобы его десятичная запись оканчивалась одной из цифрой 0 или 5.

4: для того, чтобы число х делилось на 4, необходимо и достаточно чтобы на 4 делилось двузначное число образованные последними двумя цифрами десятичной записи числа х.

25: для того, чтобы число х делилось на 25, необходимо и достаточно чтобы на 25делилось двузначное число образованные последними двумя цифрами десятичной записи числа х.

8: для того, чтобы число х делилось на 8, необходимо и достаточно чтобы на 8 делилось трехзначное число образованные последними тремя цифрами десятичной записи числа х.

125: для того, чтобы число х делилось на 125, необходимо и достаточно чтобы на 125 делилось трехзначное число образованные последними тремя цифрами десятичной записи числа х.

9: для того, чтобы число х делилось на9, необходимо и достаточно чтобы сумма цифр его десятичной записи делилась на 9.

3: для того, чтобы число х делилось на 3, необходимо и достаточно чтобы сумма цифр его десятичной записи делилась на 3.

Докажем признак делимости на 2.

Пусть число х записано в десятичной системе счисления, т.е.
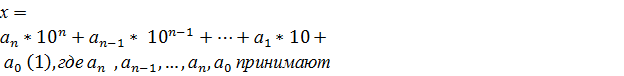значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и
и

Так как 10

как сумму двух слагаемых, каждое из которых делится на 2. Следовательно, согласно теореме о делимости суммы и само число х делится на 2.

Докажем теперь обратное: если число х делится на 2, то его десятичная запись оканчивается одной из цифр 0, 2, 4, 6, 8.

Запишем равенство (1) в таком виде:
Но тогда по теореме о делимости разности
Чтобы однозначное число делилось на 2, оно должно принимать значения 0, 2, 4, 6, 8.