
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нахождение наибольшего общего делителя и наименьшего общего кратного чисел способом разложения на простые множители.
|
|
Представления числа в виде произведения простых чисел называется разложением этого числа на простые множители.
Например, запись 110 = 2 · 5 · 11 говорит о том, что число 110 разложено на простые множители 2, 5 и 11.
Вообще разложить на простые множители можно всякое составное число причем при любом способе получается одно и тоже разложение, если не учитывать порядка множителей. Поэтому представления числа 110 в виде произведения 2 · 5 · 11 или произведение 5 · 2 · 11 есть, по существу, одно и тоже разложения числа 110 на простые множители.
Раскладывая числа на простые множители, используя признаки деления на 2, 3, 5 и др. вспомним способ записи разложения числа на простые множители. Разложим, например на простые множители число 720. Число 720 делится на 2. Значит, 2 есть один из простых множителей в разложении числа 720. Разделим 720 на 2. Число 2 пишется справа от знака равенства, а частное 360 – под числом 720. Число 360 делим на 2, получаем 180. Делим 180 на 2, получаем 90, делим 90 на 2, получаем 45, делим 45 на 3, получаем 15, делим 15 на 3, получаем 5. Число 5 простое, при делении его на 5 получаем 1. Разложение на множители закончено.
720 = 2 · 2 · 2 · 2 · 3 · 3 · 5
Произведение одинаковых множителей принято заменить степенью: 720 =  · 5. Такое представление числа 720 называют каноническим видом этого числа.
· 5. Такое представление числа 720 называют каноническим видом этого числа.
Разложения числа на простые множители используется при нахождении их наибольшего общего делителя и наименьшего общего кратного.
Найдём, например, наибольший общий делитель и наименьшее общее кратное чисел 3600 и 288.
Представим каждое из данных чисел в каноническом виде.
3600 = 2 · 2 · 2 · 2 · 3 · 3 · 5 · 5 = 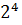 ·
·  ·
· 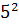 ; 288 = 2 · 2 · 2 · 2 · 2· 3 · 3 =
; 288 = 2 · 2 · 2 · 2 · 2· 3 · 3 =  ·
· 
1800 144
900 72
450 36
225 18
75 9
25 3
5 1
В разложении на простые множители наибольшего общего делителя чисел 3600 и 288 должны войти всё общи простые множите, которые содержатся в разложениях данных чисел, причем каждый из них нужно взять с наименьшим показателем, с каким он входит в оба разложения. Поэтому в разложение наибольшего общего делителя чисел 3600 и 288 войдут множители 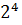 и
и  . Значит, D (3600? 288) =
. Значит, D (3600? 288) = 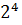 ·
·  = 144.
= 144.
В разложении на простые множители наименьшего общего кратного чисел 3600 и 288 должны войти все простые множители, которые содержатся хотя бы в одном из разложений чисел 3600 и 288 причем каждый из них нужно взять с наибольшим показателем, входящим в оба разложения данных чисел. Поэтому в разложение наименьшего общего кратного чисел 3600 и 288 войдут множители  ,
,  , 5. Значит,
, 5. Значит,
К (3600, 288) =  ·
·  · 5 = 7200.
· 5 = 7200.
Вообще чтобы найти наибольший общий делитель данных чисел:
1) Представляем каждое данное число в каноническом виде;
2) Образуем произведение общих для всех данных чисел простых множителей, причем каждый из них берём с наименьшим показателем, с каким он входит во все разложения данных чисел;
3) Находим значение этого произведения – оно и будет наибольшим общим делителем данных чисел.
Чтобы найти наименьшее общее кратное данных чисел:
1) Представляем каждое данное число в каноническом виде;
2) Образуем произведение из всех простых множителей, находящихся в разложениях данных чисел, причем каждый берем с наибольшим показателем, с каким он входит во все разложения данных чисел;
3) Находим значение этого произведения – оно и будет наименьшим общим кратным данных чисел.