Контрольная работа. 1 На биссектрисе первого координатного угла лежат точки и , расстояние между которыми равно

Вариант 1

1 На биссектрисе первого координатного угла лежат точки и 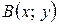, расстояние между которыми равно 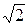. Найти координаты точки .

2 Найти уравнение прямой, проходящей через точку пересечения прямых и 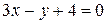параллельно прямой .

3 Найти угол между высотой 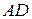и медианой в треугольнике с вершинами в точках , , .

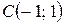4 Найти каноническое уравнение эллипса, если

а) расстояние между концами большой и малой оси равно 5, а сумма длин полуосей равна 7;

б) расстояние от его фокуса до концов большой оси равны 2 и 14.

5 Через фокус параболы проведена прямая под углом 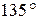к оси 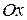. Найти длину образовавшейся хорды.

Вариант 2

1 Дан треугольник с вершинами 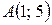, , 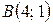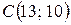. Найти точку пересечения биссектрисы внутреннего угла со стороной .

2 Прямая удалена от начала координат на расстояние . Найти значение .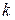

3 Даны последовательные вершины параллелограмма 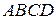: , , 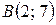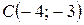. Найти координаты четвертой вершины 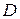и написать уравнение диагонали .

4 Найти уравнение прямой, содержащей диаметр окружности 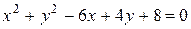, перпендикулярный прямой .

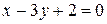5 Найти уравнение гиперболы, зная, что ее эксцентриситет 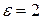, фокусы гиперболы совпадают с фокусом эллипса .

Вариант 3

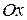1 Найти координаты центра и радиус окружности, проходящей через точку и касающейся оси в точке .

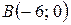2 Написать уравнение прямой, проходящей через точку 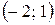на расстоянии 1 от начала координат.

3 При каких значениях и 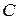прямая :

а) параллельна прямой ;

б) перпендикулярна прямой ;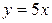

в) проходит через точк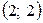и и ;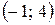

г) пересекается с прямой .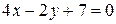

4 Найти площадь четырехугольника, две вершины которого лежат в фокусах эллипса , а две другие совпадают с концами его малой оси.

5 Найти длину диаметра эллипса (хорды, проходящей через центр эллипса) 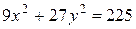, перпендикулярного к асимптоте гиперболы 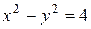, проходящей через первую и третью четверти.

Вариант 4

1 Площадь треугольника с вершинами , , 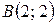равна 15. Найти ординату вершины .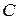

2 Через точку пересечения прямых 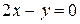и проведена прямая, перпендикулярная прямой 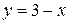. Найти ее уравнение.

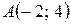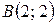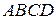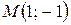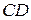3 Даны две смежные вершины , параллелограмма и точка пересечения его диагоналей. Найти уравнения сторон и параллелограмма.

4 Окружность проходит через точки и 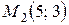, а центр ее лежит на прямой . Найти уравнение окружности.

5 Дан эллипс . Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах данного эллипса.