Полярная система координат. Переход от полярной системы координат к декартовой и обратно. Построение кривой, определяемой уравнением в полярных координатах

В полярной системе координат основными постоянными элементами, по отношению к которым определяется положение точки на плоскости, являются точка 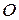- полюс и ось 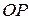, которая называется полярной осью.

Если 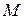- произвольная точка плоскости, не совпадающая с полюсом 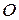, то ее положение на плоскости вполне определено заданием двух чисел: - ее расстояние от полюса, выраженного в ед. масштаба, и - угла, на который следует повернуть полярную ось против часовой стрелки, чтобы она совпадала с лучом. Из них первой координатой считается , а второй . Координата называется полярным радиусом точки 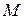(иногда радиусом-вектором точки 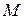), а координата - ее полярным углом*.

Полярный угол считается положительным, если он отсчитывается от полярной оси против часовой стрелки, и отрицательным, если он отсчитывается от полярной оси по часовой стрелке.

Если полюс полярной системы координат находится в начале прямоугольной системы координат, а положительная полуось 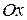совпадает с полярной осью, ось же 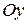перпендикулярна оси 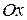и направлена так, что ей соответствует полярный угол 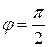, то по известным полярным координатам точки ее прямоугольные координаты 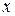и 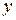вычисляются из формул

, .

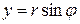Если же известны прямоугольные координаты 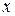и 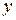точки, ее полярные координаты определяются по формулам

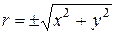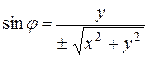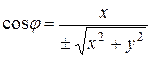; ; ; (55)