Классификация моделей

В зависимости от выбранных средств моделирования модель может быть:

a) абстрактной (концептуальной):

- словесная (вербальная) модель, представляемая словесным описанием явлений и взаимосвязей;

- числовая модель как совокупность значений числовых характеристик объекта (процесса);

- математическая модель, описывающая процессы посредством математических выражений;

- графическая модель, отображающая процессы графическими средствами (образами);

b) материальной (физической):

- натурная;

- макет;

- аналоговая модель, в которой физическая природа модели и объекта различны, а их математические описания подобны.

Для описания социально-экономических систем приемлемы лишь абстрактные модели.

Пример 2.4. Тенденция, именуемая в маркетинге “ законом спроса ”, может быть отображена следующими абстрактными моделями:

a) вербальной:

“С увеличением цены, назначаемой продавцом, спрос на товар снижается”;

b) числовой:

Цена за единицу, у.е. Спрос на товар, шт./период

10 180

20 160

30 140

50 100

80 40

c) математической:

,

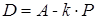где

D - спрос на товар – это зависимая (объясняемая) переменная;

P - цена единицы товара – это независимая (объясняющая) переменная;

A, k - параметры (коэффициенты) уравнения;

d) графической:

Рис. 2.3. Кривая спроса (для большинства товаров)

Модели, при построении которых преследуется цель определения такого состояния объекта, которое является наилучшим в каком-то смысле или допустимым с точки зрения субъекта моделирования, называются оптимизационными. Без таких моделей, дающих ответ на вопрос “Как или сколько должно быть? ”, не обойтись в процессе выработки и принятия рациональных решений.

Структурно любая оптимизационная модель представляется как минимум двумя элементами:

целевой функцией (формальное описание критерия оптимальности) и

системой ограничений в виде равенств и неравенств, накладываемых на переменные целевой функции.