Задачи эконометрики

В большинстве случаев экономические законы выражаются в относительно простой математической форме.

Рассмотрим, например, функцию потребления:

или в линеаризованном виде

,

где

C - потребление некоторого пищевого продукта на душу населения в некотором году;

Y - реальный доход на душу населения в этом году;

P - индекс цен на этот продукт, скорректированный (дефлированный) на общий индекс стоимости жизни;

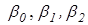- константы (коэффициенты, параметры).

Это уравнение называется уравнением поведения. Оно описывает (в среднем) поведение потребителя по отношению к покупке данного пищевого продукта в зависимости от относительного уровня цен на продукт и реального душевого дохода. Закон поведения будет определен, как только мы найдем значения параметров .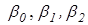

Важнейшая задача эконометрики – оценить параметры из подходящего набора выборочных наблюдений.

Не определить точно, а оценить!

Определить – это вычислить.

Оценить – это установить значение, наиболее близкое к действительному (например, «оценить уровень знаний»).

Цель любого оценивания – получить как можно более точное значение неизвестной характеристики генеральной совокупности (генеральная совокупность содержит множество всех возможных исходов интересующих экономических показателей). Информацией, которой мы при этом располагаем, являются данные выборочного наблюдения, т.к. на практике можно наблюдать только случайно выбранные значения интересующих показателей.

При выборочном наблюдении обследованию подлежат не все элементы совокупности, а только специально отобранная их часть.

Желательные свойства оценок параметров модели

Пусть на основе выборки объема n определяется оценка истинного значения параметра b генеральной совокупности.

Для того чтобы выборочная оценка давала хорошее приближение оцениваемого параметра, она должна удовлетворять следующим требованиям.

Несмещенность оценки.

Оценка называется несмещенной, если математическое ожидание такой оценки при любом объеме выборки равно истинному значению параметра:

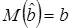
При использовании несмещенной оценки мы не получаем систематической ошибки, т.е. ошибки постоянной по величине и знаку.

Состоятельность оценки.

Оценка называется состоятельной, если при увеличении числа наблюдений она приближается к истинному значению параметра:

Если дисперсия несмещенной оценки при стремится к нулю, то такая оценка является и состоятельной.

Эффективность оценки.

Несмещенная оценка не всегда дает «хорошее» приближение оцениваемого параметра. Возможные значения оценки неизвестного параметра могут быть сильно рассеяны вокруг своего среднего значения, если дисперсия оценки значительна. В этом случае найденная по данным одной выборки оценка может оказаться удаленной от оцениваемого параметра. Поэтому следует потребовать, чтобы дисперсия оценки параметра была малой. Это требование называется требованием эффективности оценки.

Оценка называется эффективной, если дисперсия оценки является наименьшей при данном размере выборки, т.е. разброс этой оценки относительно истинного значения минимально возможный:

Оценка параметров модели – важнейшая, но не единственная задача эконометрики.

Перед решением этой задачи выясняются следующие вопросы:

1) о возможности и необходимости присутствия в модели тех или иных переменных,

2) о форме их взаимосвязи,

3) о характере модели (статическая или динамическая).

Ответив на эти вопросы, мы тем самым решаем еще одну важную задачу эконометрики – задачу спецификации модели.

Возвращаясь к вопросу определения закона поведения, можно, например, задать следующие вопросы, также относящиеся к эконометрике:

- нет ли переменных, которые следовало бы дополнительно включить в уравнение (например, цены на непродовольственные товары);

- не следует ли исключить из уравнения некоторые переменные (модели должны быть «настолько простыми, насколько возможно, но не проще», сказал Эйнштейн);

- насколько корректно измерены данные, представляют ли они то, что должны представлять по нашему мнению;

- верно ли, что модель линейна;

- верна ли экономическая теория;

- является ли модель полной (в данном примере мы имеем дело с уравнением спроса и не принимаем во внимание уравнение предложения; что произойдет, если мы будем изучать спрос и предложение одновременно);

- достаточно ли изучать макроэкономическое уравнение, подобно приведенному выше, для ответа на интересующие нас вопросы, или необходимо изучать также индивидуальные (микро) данные;

- приведенная выше модель является статической. Возможно, более подходящей была бы динамическая модель. Например, можно предположить, что прошлогодний доход может влиять на текущий уровень потребления. В этом случае мы должны также включить его в уравнение.