Эконометрическая модель

Основным понятием в эконометрики является эконометрическая модель.

Эконометрические модели – это модели, количественно описывающие взаимосвязи между экономическими показателями.

В частности, эконометрическая модель – это математическое описание того, что (исходя из предварительного анализа) экономическая теория считает наиболее важным при исследовании данной проблемы.

Эконометрическая модель (в отличие от модели математической экономики) носит конкретный характер и представляет параметры (коэффициенты) в численном виде. Следовательно, задача эконометрики – на основе имеющихся наблюдений (реальной статистической базы) оценить эти параметры (коэффициенты).

Состав эконометрической модели

Основу эконометрической модели составляет система регрессионных уравнений, каждое из которых отображает одну из зависимостей, одну из закономерностей изменения, одно из свойств изучаемых экономических процессов. Помимо регрессий в модель могут быть включены:

- выражения, описывающие тренды развития отдельных явлений;

- тождества, характеризующие балансовые увязки между переменными;

- уравнения, увязывающие между собой отдельные характеристики модели во времени (динамический вариант модели).

Модель содержит также различного рода параметры (коэффициенты), которые определяются в ходе статистического оценивания путем обработки имеющихся данных наблюдения.

Уравнения-тождества – это соотношения, которые должны выполняться во всех случаях (тождества не содержат подлежащие оценке параметры и случайные составляющие). Например, модель спроса и предложения (см. пример 2.6) содержит тождество .

Таким образом, эконометрическая модель представляет собой результат статистического оценивания параметров системы математических выражений, которые характеризуют некоторую экономическую концепцию о взаимосвязи явлений.

Классификация переменных эконометрической модели

Эконометрическая модель содержит так называемые эндогенные и экзогенные переменные. Приставки «эндо» и «экзо» означают соответственно внутренние и внешние.

Эндогенными переменными являются те, значения которых выясняются на основе (внутри) модели. Это зависимые переменные.

Экзогенные переменные – это переменные, значения которых определяются вне модели. Это переменные, влияющие на эндогенные переменные, но не зависящие от них.

Эндогенные и экзогенные переменные могут быть как обычными, так и лаговыми.

Значения обычной переменной соответствуют рассматриваемому периоду времени. Под лаговой переменной понимают переменную, значения которой отстают на один или несколько периодов (если 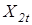– значения обычной переменной, то – её лаговые значения, смещенные на один период). Лаговые (эндогенные и экзогенные) и обычные экзогенные переменные образуют множество предопределенных переменных.

Совместно зависимыми переменными называются обычные эндогенные переменные, которые объясняются эконометрической моделью в момент времени t.

Классификация переменных представлена на рис.2.6.

Пояснения на примере модели «спрос-предложение»: равновесная цена товара 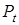и спрос на товар 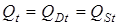определяются из уравнений модели, т.е. являются обычными эндогенными переменными. Предопределенными переменными в данной модели являются доход 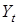(обычная экзогенная переменная) и цена товара в предыдущий момент времени (лаговая эндогенная переменная).

Рис. 2.6. Классификация переменных эконометрической модели

Структурная и приведенная формы эконометрической модели

Взаимозависимые (одновременные) модели имеют две формы: структурную и приведенную.

Структурной формой модели (системой одновременных уравнений) называется система уравнений, в каждом из которых помимо объясняющих переменных могут содержаться объясняемые переменные из других уравнений.

Структурная форма модели создается в процессе формирования самой модели при стремлении отразить причинно-следственный механизм, существующий в реальности.

Параметры (коэффициенты) уравнений модели в структурной форме называются структурными коэффициентами. Использование обычного метода наименьших квадратов для оценивания параметров структурных уравнений, каждого в отдельности, приведет в общем случае к получению смещенных и несостоятельных оценок.

Метод наименьших квадратов (МНК) – построение аппроксимирующей функции из условия минимизации суммы квадратов отклонений значений этой функции от полученных (наблюдаемых) значений при заданном аргументе.

Аппроксимация функций – это приближенное выражение одних функций другими. Например, (синус Х приблизительно равен Х при Х близком к нулю).

По предположению система уравнений структурной формы модели должна быть совместной и, следовательно, она может быть решена относительно обычных эндогенных переменных. Результат решения представляет собой приведенную форму модели.

Приведенной формой модели называется система уравнений, в каждом из которых обычные эндогенные переменные выражены только через предопределенные переменные и случайные составляющие.

Пример 2.7. Приведенная форма модели спроса и предложения:

- Цена товара

- Спрос на товар

Уравнения приведенной формы позволяют получить значения обычных эндогенных переменных, однако они объясняют эти значения только через экзогенные (в общем случае – предопределенные) переменные, т.е. с существенно меньшей детализацией, чем структурная форма, – здесь отсутствуют взаимосвязи зависимых переменных между собой. Параметры приведенной формы модели называются коэффициентами приведенной формы. Коэффициенты приведенной формы могут быть оценены обычным МНК, причем к каждому уравнению этот метод применяется раздельно.