Классификация математических моделей для анализа и прогноза

Выделяют три основных класса математических моделей, которые применяются для анализа и/или прогноза.

1. Модели временных рядов.

В этих моделях зависимая переменная Y представляется в виде функции только одной независимой переменной, причем в качестве этой одной независимой переменной выступает время t.

К этому классу относятся модели:

- Тренда:

Тренд – изменение, определяющее общее направление развития, основную тенденцию временных рядов.

,

где

- временной тренд заданного параметрического вида.

Например, линейный ;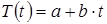

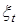- случайная (стохастическая) компонента.

- Сезонности:

,

где

- периодическая (сезонная) компонента.

- Тренда и сезонности:

- аддитивная;

- мультипликативная.

Общая черта моделей временных рядов – они объясняют поведение временного ряда, исходя только из его предыдущих значений. Такие модели могут применяться, например, для изучения и прогнозирования:

- объема продаж авиабилетов;

- спроса на мороженое;

- краткосрочного прогноза процентных ставок и т.п.

2. Регрессионные модели с одним уравнением.

В таких моделях зависимая (объясняемая) переменная Y представляется в виде функции одной или нескольких независимых (объясняющих) переменных:

,

где

-

функция (функциональная составляющая зависимости);

- независимые (объясняющие) переменные;

- параметры;

- случайная величина.

В зависимости от вида функции модели делятся на линейные и нелинейные.

Например, можно исследовать:

- спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов;

- зависимость зарплаты от возраста, пола, уровня образования, стажа работы и т.п.

Область применения таких моделей, даже линейных, значительно шире, чем моделей временных рядов.

3. Системы одновременных уравнений.

Эти модели описываются системами уравнений.

Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы, т.е. зависимые переменные одних уравнений могут выступать в качестве независимых переменных других. Таким образом, мы имеем здесь набор объясняемых переменных, связанных через уравнения системы. Поэтому такие модели называются взаимозависимыми (или одновременными).

Примером может служить модель спроса и предложения, приведенная ниже.

Пример 2.6. Модель спроса и предложения.

Пусть 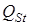- предложение товара в момент времени t;

- спрос на товар в момент времени t;

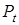- цена товара в момент времени t;

- цена товара в предыдущем периоде;

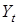- доход в момент времени t;

- случайные компоненты.

Составим следующую систему уравнений «спрос - предложение»:

(предложение)

(спрос)

(равновесие рынка)

Из уравнений модели определяются равновесная цена товара 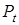и равновесный спрос на товар .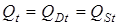