
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Спосіб векторних діаграм – графічне зображення гармонічного руху. Перш ніж розглядати додавання коливальних рухів, спинимося на способі подачі коливань з допомогою обертового вектора амплітуди
|
|
Перш ніж розглядати додавання коливальних рухів, спинимося на способі подачі коливань з допомогою обертового вектора амплітуди. Нехай гармонічний коливальний рух описується рівнянням:
 (16)
(16)
Проведемо пряму лінію  , яку умовно назвемо «опорною», і побудуємо вектор
, яку умовно назвемо «опорною», і побудуємо вектор  , що чисельно дорівнює амплітуді
, що чисельно дорівнює амплітуді 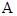 і напрямлений з точки
і напрямлений з точки 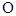 під кутом
під кутом  до опорної лінії (рис.1). Якщо початкова фаза додатна, то кут
до опорної лінії (рис.1). Якщо початкова фаза додатна, то кут  відкладається від опорної лінії в бік, протилежний обертанню годинникової стрілки; якщо початкова фаза від’ємна, то кут
відкладається від опорної лінії в бік, протилежний обертанню годинникової стрілки; якщо початкова фаза від’ємна, то кут  відкладається за годинниковою стрілкою. Проекція вектора
відкладається за годинниковою стрілкою. Проекція вектора  на опорну лінію дорівнює зміщенню
на опорну лінію дорівнює зміщенню  у момент початку відліку часу
у момент початку відліку часу  :
:
 (17)
(17)
 |
Рис.1
Обертатимемо вектор амплітуди навколо осі 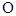 , перпендикулярної до площини рисунка, з кутовою швидкістю
, перпендикулярної до площини рисунка, з кутовою швидкістю 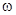 (проти стрілки годинника, якщо
(проти стрілки годинника, якщо  ). За проміжок часу
). За проміжок часу 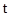 вектор амплітуди повернеться на кут
вектор амплітуди повернеться на кут  і займе положення, подане на рис.1 вектором
і займе положення, подане на рис.1 вектором 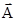 . Його проекція
. Його проекція  на опорну лінію дорівнює:
на опорну лінію дорівнює:
 (18)
(18)
За час  , що дорівнює періоду коливань, вектор амплітуди повернеться на кут
, що дорівнює періоду коливань, вектор амплітуди повернеться на кут  , а проекція
, а проекція  його кінця зробить одне повне коливання навколо положення рівноваги
його кінця зробить одне повне коливання навколо положення рівноваги  . Отже, обертовий вектор амплітуди повністю характеризує гармонічне коливання. Зображенням гармонічних коливань за допомогою обертових векторів широко користуються при вивченні додавання коливань.
. Отже, обертовий вектор амплітуди повністю характеризує гармонічне коливання. Зображенням гармонічних коливань за допомогою обертових векторів широко користуються при вивченні додавання коливань.
Замість тригонометричних функцій для опису коливальних процесів також використовують показникові функції Ейлера виду
 (19)
(19)
Дійсна частина  являє собою тригонометричну функцію
являє собою тригонометричну функцію  . Як правило, обчислення ведуться з показниковими функціями і при необхідності результат подають у тригонометричній формі.
. Як правило, обчислення ведуться з показниковими функціями і при необхідності результат подають у тригонометричній формі.
Так, якщо  , то
, то  . Для переходу від амплітуди коливань
. Для переходу від амплітуди коливань  до виразів енергії, потрібно знайти квадрат амплітуди. Для цього треба
до виразів енергії, потрібно знайти квадрат амплітуди. Для цього треба  помножити на спряжений вираз
помножити на спряжений вираз  . Тоді отримаємо
. Тоді отримаємо  .
.