Методики расчета тарифных ставок

Распоряжением № 02-03-36 от * июля 1993 г. Росстрахнадзор утвердил две методики расчета тарифных ставок по рисковым видам страхования.

Первая методика применяется при следующих условиях:

1) существует информация, позволяющая оценить следующие величины по рассматриваемому виду страхования:

- P(A) – вероятность наступления страхового случая А по договору страхования

(2)

- - средняя страховая сумма по договору страхования

, (3)

где - страховая сумма при заключении i – ого договора;

- - среднее возмещение при наступлении страхового случая по договору страхования

, (4)

где - страховое возмещение, выплачиваемое при наступлении страхового случая по k – ому договору страхования;

2) предполагается, что не будет опустошительных событий;

3) страхованием охватывается значительное число субъектов страхования и страховых рисков, причем страхуемые объекты отличаются однородностью, а разброс страховых сумм не велик;

4) расчет тарифов производится при заранее известном количестве договоров n, которые предполагается заключить со страхователем.

Последовательность расчета тарифной ставки по этой методики такова:

1) Брутто-ставка (Т_б) рассчитывается по формуле:

, (5)

2) Нетто-ставка (Т_н) состоит из основной части (Т_о) и рисковой надбавки (Т_р), т.е.

, (6)

3) зависимости от исходных данных Т_о может находиться несколькими способами:

, (7)

, (8)

, (9)

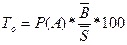, (10)

где P(A) – вероятность наступления страхового случая А.

4) расчет рисковой надбавки может осуществляться:

- при отсутствии данных о разбросе (среднеквадратическом отклонении) возможных страховых выплат (R)

(11)

- при наличии данных о разбросе возможных сумм страхового возмещения

, (12)

где - коэффициент, который зависит от гарантии безопасности . Его значение берется из таблицы 3.

Таблица 3

Значение коэффициента , зависящего от гарантии безопасности

	0, 84	0, 90	0, 95	0, 98	0, 9986
	1, 0	1, 3	1, 645	2, 0	3, 0

Пример 1. Вероятность наступления страхового случая равна 0, 01; средняя страховая сумма – 7 тыс. руб.; среднее страховое возмещение – 700 руб.; доля нагрузки в структуре тарифа – 30%. Рассчитать тарифную ставку договоров имущественного страхования с учетом рисковой надбавки в нетто-ставке, если требуется обеспечить гарантию достаточности страховых взносов на уровне 95% и известно, что число предполагаемых договоров страхования составит 500 ед.