Решение. 1) вероятность наступления страхового случая по формуле (2)

Дано:

m=240 ед.

B= 12000 тыс. руб.

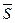= 90 тыс. руб.

n = 8000 ед.

Н = 25%

R = 8 тыс. руб.

= 0, 90

Определяем:

1) вероятность наступления страхового случая по формуле (2)

2) страховую сумму по всем заключенным договорам

= 90*8000 = 720000 тыс. руб.

3) основную часть нетто-ставки по формуле (8)

руб. на 100 руб. S

4) среднее страховое возмещение, выплаченное по 1 договору страхования

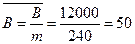тыс. руб.

5) рисковую надбавку по формуле (12)

= руб. на 100 руб. S

6) нетто-ставку по формуле (6)

1, 67+0, 14 = 1, 81 руб. на 100 руб. S

7) брутто-ставку по формуле (5)

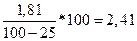= руб. на 100 руб.S

Примечание: основную часть нетто-ставки можно определить по формуле (10)

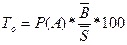= руб. на 100 руб. S

Ответ: тарифная ставка при страховании от несчастного случая составляет 2, 41 руб. на 100 руб. страховой суммы или 2, 41%.

Вторая методика используется для определения прогнозной тарифной ставки по отдельным видам рисков. Эта методика применима:

· при наличии информации о сумме страхового возмещения и совокупной страховой сумме по рискам, принятым на страхование за ряд лет (не менее пяти);

· когда зависимость убыточности страховой суммы от времени близка к линейной.

Суть второй методики сводится к следующему:

1) находят убыточность страховой суммы по формуле (7);

2) прогнозируют убыточность страховой суммы на основе модели линейного тренда

, (13)

где t – порядковый номер соответствующего года;

а₀ – среднегодовая убыточность страховой суммы;

а₁ – среднегодовой прирост страховой суммы на 100 руб. S.

Параметры а₀ и а₁ находятся методом наименьших квадратов, в результате которого получают следующую систему нормальных уравнений:

(14)

где n – число анализируемых лет.

Данную систему уравнений можно упростить, если начать отчет лет не с начала ряда, а с середины, таким образом, чтобы (если ряд четный, то …-2, -1, 1, 2, …, если ряд нечетный, то …-2, -1, 0, 1, 2, …). Тогда система уравнений (14) примет следующий вид:

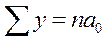
(15)

Примечание: параметры уравнения тренда можно определить с помощью Microsoft Excel (Сервис - пакет анализа – анализ данных – регрессия).

3) определяют выровненную убыточность страховой суммы для каждого года путем подстановки значений для каждого года в уравнение (13);

4) находят прогнозный уровень убыточности страховой суммы на следующий год , подставив в уравнение (13) ;

5) рассчитывают рисковую надбавку по формуле среднеквадратического отклонения:

; (16)

6) определяют нетто-ставку по формуле:

; (17)

7) определяют брутто-ставку по формуле (5).

Пример 3. На основе имеющихся данных об убыточности страховой суммы за последние 5 лет (табл.4) определить брутто- ставку на следующий год при страховании имущества граждан. Уровень гарантии безопасности составляет 90%, а доля нагрузки в структуре тарифа – 20%.

Таблица 4

Динамика убыточности страховой суммы

Показатели	Годы
Фактическая убыточность страховой суммы, %()	3, 0	2, 9	3, 2	3, 1	3, 3