
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Первый закон термодинамики
|
|
Первый закон (первое начало) термодинамики в общем виде представляет собой закон сохранения и превращения энергии. Этот закон налагает строгое условие на все процессы природы, которые при всем их разнообразии ограничены условием сохранения энергии. Дадим несколько формулировок первого закона.
1. Все виды энергии могут взаимно превращаться в строго равных друг
другу количествах, т.е. энергия не возникает из ничего и не исчезает, а переходит из одного вида в другой. При переходе механической энергии в теплоту ее отношение к соответствующему количеству теплоты называется термическим эквивалентом работы, который равен J=L/Q= 4, 1868 Дж/кал, если
работа измеряется в Джоулях, а теплота в калориях. Если теплота и работа
измеряются в одних единицах, то J =1. Величина, обратная термическому эквиваленту работы, называется механическим эквивалентом теплоты A=1/J=Q/L.
2. Невозможно построить такую периодически действующую машину, с
помощью которой можно было бы получить полезную работу без затраты
энергии извне, т.е., черпая энергию из ничего. Подобное устройство называется вечным двигателем первого рода, построение и работа которого в соответствии с законом сохранения энергии невозможно.
3. Внутренняя энергия полностью изолированной системы есть величина постоянная. Доказательство этой формулировки будет дано ниже.
Запишем уравнение первого закона термодинамики. Для этого допустим, что к телу подведено некоторое количество теплоты Q. Эта теплота будет затрачена на изменение внутренней энергии Δ U и на совершение работы L. Тогда для m кг массы тела уравнение эквивалентности будет
 (2.16)
(2.16)
где Q=mq; Δ U = m Δ u; L=ml.
Для одного кг массы (m =1) соотношение (2.16) примет вид

где q, Δ u, l - удельные количества теплоты, изменения внутренней энергии и работы.
Для бесконечно малого процесса
 (2.17)
(2.17)
Соотношение (2.17) представляет из себя математическую запись уравнения первого закона термодинамики. Из этого уравнения следует, что теплота, подведенная к рабочему телу, затрачивается на изменение внутренней энергии и на совершение работы.
Применим к уравнению (2.17) условия полной изоляции, т.е. dq =0 и dl =0 (система не обменивается с окружающей средой ни теплотой, ни работой). Тогда получим du =0 или u =const, т.к. дифференциал постоянной равен нулю. Таким образом, мы доказали, что какие бы процессы не происходили в изолированной системе, ее внутренняя энергия есть величина постоянная.
Определим правило знаков для количества теплоты q. Если она подводится к телу, то q > 0. Работа l > 0, если она совершается расширяющимся газом и l < 0, если работа затрачивается на сжатие. Изменение внутренней энергии Δ u > 0, если внутренняя энергия тела увеличивается, и наоборот.
Найдем выражение работы через основные параметры состояния (см. рис. 2.4.).
При бесконечно малом перемещении поршня вправо работа 1 кг газа будет dl=pSdr, где р - давление в точке 3; S - площадь поперечного сечения поршня; r - перемещение поршня. Так как Sdr=dv, то
 (2.18)
(2.18)
Из формулы (2.18) следует, что работа есть площадь под элементарным участком процесса 1-2. Работа всего процесса 1-2 будет равна площади под кривой этого процесса, т.е. площади v 1 1 3 2 v 2 v 1.

Рис. 2.4
Для того чтобы найти явное выражение для работы, следует проинтегрировать уравнение (2.18)
 (2.19)
(2.19)
Ввиду того, что работа является функцией процесса, а не функцией состояния, то дифференциал dl от работы не является полным дифференциалом. В связи с чем некоторые авторы [13] вводят специальное обозначение для бесконечно малого приращения количества работы δ l и количества теплоты δ q, дифференциал которой также не является полным дифференциалом (подробнее см. § 2.10). В настоящей книге мы будем придерживаться обозначений, принятых в большинстве учебников по термодинамике.
С целью упрощения расчетов многих термодинамических процессов У.Гиббсом введена функция I (для m кг массы) и i (для 1 кг), называемая энтальпией. Эта функция вводится по формуле
 (2.20)
(2.20)
Так как u, р и v - функции состояния, то энтальпия i также будет функцией состояния.
Продифференцируем соотношение (2.20)
 (2.21)
(2.21)
Выражая из (2.21) du и подставляя в (2.17) с учетом (2.18), получим
 (2.22)
(2.22)
где –vdp = dl0 - располагаемая работа.
Интегрируя (2.22), находим

Для вывода формулы располагаемой работы рассмотрим процесс, изображенный на рис. 2.5.

Рис. 2.5
Здесь линия с -1 соответствует процессу наполнения цилиндра двигателя рабочим телом. Работа, совершаемая внешней средой над рабочим телом, будет равна l1=p1v1, т.е. площади 0- с -1-а. Эта работа положительна. Линия 1-2 является процессом расширения рабочего тела. Здесь совершается работа расширения

Линия 2- d соответствует выталкиванию рабочего тела из цилиндра двигателя. Эта работа затрачивается - она отрицательна и равна l2=p2v2.
Алгебраическая сумма всех перечисленных выше работ графически равна заштрихованной площади с -1-2- d, которая и представляет располагаемую работу l0 с учетом работы поступления и удаления рабочего тела из машины, т.е.
l0 = пл. c -1-2- d = пл. 0- c -1- a + пл. a -1-2- b – пл. 0- d -2- b =
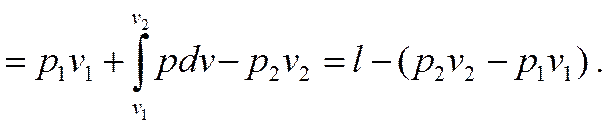
Отсюда
 (2.23)
(2.23)
Подставляя (2.23) в уравнение первого закона термодинамики, записываемого для конечного процесса q = Δ u + l, получим

Отсюда
 (2.24)
(2.24)
Полученное уравнение совпадает с уравнением (2.22). Это уравнение представляет вторую математическую форму записи уравнения первого закона термодинамики.
Если в термодинамическом процессе давление остается постоянным, то уравнение (2.22) примет вид

Или для конечного процесса

Таким образом, физический смысл энтальпии состоит в том, что в изобарных процессах изменение энтальпии равно количеству теплоты, поглощенной или отданной системой.
В случае отсутствия теплообмена с окружающей средой (адиабатные процессы, dq= 0) уравнение (2.22) будет

или

Следовательно, при dq = 0 располагаемая работа равна разности энтальпий начала и конца процесса.
Ввиду того, что энтальпия является функцией независимых параметров состояния, то для ее полного дифференциала справедливы соотношения соответственно при независимых переменных v, р; v, Т и р, Т.


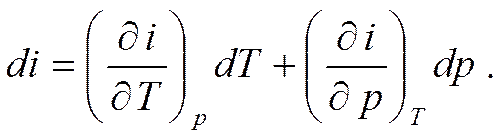
Энтальпия идеального газа, также как и внутренняя энергия, является функцией только температуры и не зависит от объема и давления, т.к. отсутствуют силы взаимодействия между молекулами.
