Термические коэффициенты и связь между ними

Термические коэффициенты характеризуют тепловые и упругие свойства тел.

Известны коэффициент объемного расширения α, термический коэф­фициент давления β и изотермический коэффициент сжимаемости γ.

При нагревании определенной массы вещества при постоянном внешнем давлении изменение объема на каждый градус повышения температуры вы­ражается частной производной (dV/dT) _p. Относительное изменение объема при нагревании на один градус называется коэффициентом объемного рас­ширения

(2.11)

Для идеального газа α =1/Т.

Если температуру выражать в градусах шкалы Цельсия, то dt=dT и отно­сительное изменение объема можно представить отношением производной 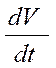к объему V₀ при 0°С, т.е.

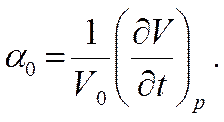
Если принять, что в небольшом интервале изменения температур α ₀=const, то

Интегрируя последнее соотношение, приходим к выводу, что объем при изменении температуры изменяется по линейному закону

Для идеального газа при любом давлении

1/ ⁰C.

Если нагревать данную массу вещества при постоянном объеме, то отно­сительное изменение давления при изменении температуры характеризуется величиной термического коэффициента давления β

(2.12)

где р - давление при температуре Т.

Для идеального газа β =α =1/ Т.

Аналогично (2.12) можно записать

При малом изменении температуры можно считать β ₀=const

После интегрирования получим p=p₀ (1 +β ₀t).

Для идеального газа β ₀=α ₀.

При изотермическом сжатии данной массы вещества отношение измене­ния объема при изменении давления на одну единицу давления к объему на­зывается изотермическим коэффициентом сжимаемости

(2.13)

Знак минус означает уменьшение объема с увеличением давления.

Для идеальных газов по закону Бойля-Мариотта V=const/p (см. § 4.4). Дифференцируя по давлению, получим

Сравнивая последнее соотношение с (2.13), имеем γ =-1/ р. Следовательно, коэффициент сжимаемости есть величина, обратная давлению.

Найдем взаимосвязь между термическими коэффициентами α, β и γ в общем случае. Полные дифференциалы давления, объема и температуры имеют вид (подробнее см. § 2.10)

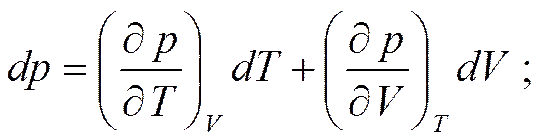
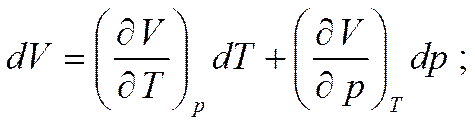
Подставляя dp из первого уравнения во второе, с учетом того, что

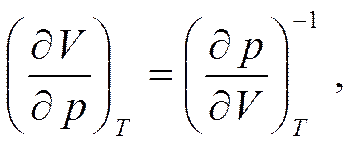
получим

(2.14)

Подставляя (2.11), (2.12), (2.13) в (2.14), будем иметь

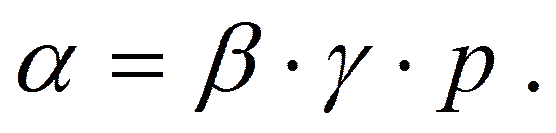(2.15)

Последнее соотношение, связывающее все три термических коэффициен­та, позволяет найти один из них, если известны два других.

Так как для идеальных газов α = β =1/ T, то из (2.15) следует, что γ =1/ p.

Для жидких тел коэффициенты сжатия очень малы. Так для воды α ₀=0, 000238, β =4, 6.

Отсюда при нормальном давлении γ ₀ =0, 000052, тогда как для газа в этом случае γ ₀ =1.

Следовательно, при увеличении давления на одну атмосферу (при t =const) объем воды убывает на 0, 000052 доли первона­чального объема.