
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Процесс ортогонализации Грама--Шмидта в конечномерном евклидовом пространстве
|
|
Определение 1. Линейное пространство конечной размерности над полем  называется унитарным, если для любых двух элементов определена комплекснозначная функция (скалярное произведение), обозначающаяся
называется унитарным, если для любых двух элементов определена комплекснозначная функция (скалярное произведение), обозначающаяся  , удовлетворяющая свойствам:
, удовлетворяющая свойствам:
- (Коммутативность)
 ;
; -
 ;
; -
 ;
; -
 -- вещественное
-- вещественное  .
.
Определение евклидова пространства отличается тем, что поле  заменяется на
заменяется на 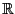 , а комплексное сопряжение в свойстве
, а комплексное сопряжение в свойстве  не требуется.
не требуется.
Теорема 1. (Грама--Шмидта) в любом конечномерном унитарном (евклидовом) пространстве можно построить ортонормированный базис.
Доказательство. Докажем методом математической индукции.
 База индукции.
База индукции. 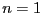 .
.  . Это и есть ОНБ.
. Это и есть ОНБ.
 Предположение. Пусть верно для
Предположение. Пусть верно для  .
.
 Доказательство индукции. Возьмем базис
Доказательство индукции. Возьмем базис  . Рассмотрим его в
. Рассмотрим его в  -мерном пространстве
-мерном пространстве  . По предположению, там найдется ОНБ
. По предположению, там найдется ОНБ  . Дополним этот базис до базиса
. Дополним этот базис до базиса  :
:  (без ограничения общности, последний вектор линейно не зависит от этого базиса). Сконструируем вектор
(без ограничения общности, последний вектор линейно не зависит от этого базиса). Сконструируем вектор
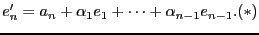
Нужно, чтобы он был ортогонален всем векторам:

а это выполнено тогда и только тогда, когда (умножая обе части равенства  на
на  последовательно)
последовательно)
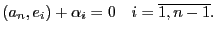
Отсюда,  ,
,  . Теперь положим
. Теперь положим  , построив тем самым ОНБ
, построив тем самым ОНБ  и доказав утрверждение теоремы.
и доказав утрверждение теоремы. 
36)
Ортогональное преобразование — линейное преобразование 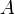 евклидова пространства
евклидова пространства 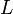 , сохраняющее длины или (что эквивалентно этому) скалярное произведение векторов. Это означает, что для любых двух векторов
, сохраняющее длины или (что эквивалентно этому) скалярное произведение векторов. Это означает, что для любых двух векторов 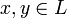 выполняется равенство
выполняется равенство

где треугольными скобками обозначено скалярное произведение  в пространстве
в пространстве 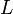 .
.
Свойства
§ Ортогональные преобразования (и только они) переводят один ортонормированный базис евклидова пространства в другой.
§ Необходимым и достаточным условием ортогональности линейного преобразования 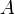 является равенство
является равенство

где  — сопряжённое, а
— сопряжённое, а  — обратное преобразования.
— обратное преобразования.
§ В ортонормированном базисе ортогональным преобразованиям (и только им) соответствуют ортогональные матрицы. Таким образом, критерием ортогональности матрицы 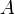 является равенство равенство (*), где
является равенство равенство (*), где  — транспонированная, а
— транспонированная, а  — обратная матрицы.
— обратная матрицы.
§ Собственные значения ортогональных преобразований равны по модулю 1, а собственные векторы (вообще говоря, комплексные), отвечающие различным собственным значениям, ортогональны.
§ Определитель ортогонального преобразования равен 1 (собственное ортогональное преобразование) или − 1 (несобственное ортогональное преобразование).
§ В произвольном n -мерном евклидовом пространстве ортогональное преобразование является композицией конечного числа отражений.
§ Множество всех ортогональных преобразований евклидова пространства образует группу относительно операции композиции — ортогональную группу данного евклидова пространства. Собственные ортогональные преобразование образуют нормальную подгруппу в этой группе (специальную ортогональную группу).
[править]Размерность два
В случае евклидовой плоскости всякое собственное ортогональное преобразование является поворотом на некоторый угол φ, и его матрица в любом ортонормированном базисе имеет вид

Матрица несобственного ортогонального преобразования имеет вид

Она симметрична, имеет собственными числами 1 и − 1 и, следовательно, является инволюцией. В подходящем ортонормированном базисе матрица несобственного ортогонального преобразования имеет вид

то есть оно является отражением относительно некоторой прямой. Собственное ортогональное преобразование есть произведение двух отражений:

[править]Размерность 3
В трёхмерном пространстве всякое собственное ортогональное преобразование есть поворот вокруг некоторой оси, а всякое несобственное — композиция поворота вокруг оси и отражения в перпендикулярной плоскости.
[править]Размерность n
Имеет место следующая общая теорема:
Для каждого ортогонального преобразования  евклидова евклидова  -мерного пространства L справедливо такое разложение -мерного пространства L справедливо такое разложение
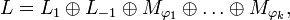 где все подпространства
где все подпространства  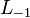 и и 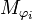 попарно ортогональны и являются инвариантными подпространствами преобразования попарно ортогональны и являются инвариантными подпространствами преобразования 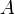 , причём:
§ ограничение , причём:
§ ограничение 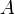 на на  есть есть  (тождественное преобразование),
§ ограничение (тождественное преобразование),
§ ограничение 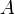 на на 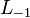 есть есть  ,
§ все пространства ,
§ все пространства 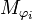 двумерны (плоскости), и ограничение двумерны (плоскости), и ограничение 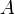 на на 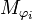 есть поворот плоскости есть поворот плоскости 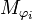 на угол φ i. на угол φ i.
|
В терминах матрицы преобразования эту теорему можно сформулировать следующим образом:
Для всякого ортогонального преобразования существует такой ортонормированный базис, в котором его матрица 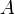 имеет блочно-диагональный вид: имеет блочно-диагональный вид:
 где
где  — матрица поворота на угол φ i (см. формулу выше), число единиц равно размерности подпространства — матрица поворота на угол φ i (см. формулу выше), число единиц равно размерности подпространства  и число минус единиц равно размерности подпространства и число минус единиц равно размерности подпространства 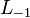 . .
|
Такая запись матрицы 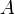 ортогонального преобразования иногда называется приведением к каноническому виду.
ортогонального преобразования иногда называется приведением к каноническому виду.
37)
38)
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Определение
Пусть 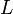 есть векторное пространство над полем
есть векторное пространство над полем  и
и  — базис в
— базис в 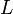 .
.
Функция 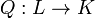 называется квадратичной формой, если её можно представить в виде
называется квадратичной формой, если её можно представить в виде

где  , а
, а  — некоторые элементы поля
— некоторые элементы поля  .
.
[править]Связанные определения
§ Матрицу  называют матрицей квадратичной формы в данном базисе. В случае, если характеристика поля
называют матрицей квадратичной формы в данном базисе. В случае, если характеристика поля  не равна 2, можно считать, что матрица квадратичной формы симметрична, то есть
не равна 2, можно считать, что матрица квадратичной формы симметрична, то есть 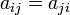 .
.
§ Для любой квадратичной формы  существует единственная симметричная билинейная форма
существует единственная симметричная билинейная форма  , такая, что
, такая, что  . Билинейную форму
. Билинейную форму  называют полярной к
называют полярной к  , она может быть вычислена по формуле
, она может быть вычислена по формуле

§ Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
§ Если матрица квадратичной формы имеет полный ранг, то квадратичную форму называют невырожденной, иначе — вырожденной.
§ Квадратичная форма  называется положительно (отрицательно) определённой, если для любого
называется положительно (отрицательно) определённой, если для любого  выполнено неравенство
выполнено неравенство 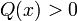
 . Положительно определённые и отрицательно определённые формы называются знакоопределёнными.
. Положительно определённые и отрицательно определённые формы называются знакоопределёнными.
§ Квадратичная форма A (x, x) называется знакопеременной, если она принимает как положительные, так и отрицательные значения.
§ Квадратичная форма  называется положительно (отрицательно) полуопределенной, если
называется положительно (отрицательно) полуопределенной, если 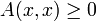
 для любого
для любого  .
.
Свойства
§ Критерий Сильвестра
§ Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
§ Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
§ Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.
§ Для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:

§ Разность между числом положительных (p) и отрицательных (n − p) членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра).
§ Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.
39)
Метод Лагранжа приведения квадратичной формы к каноническому виду
Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.
Метод Лагранжа
1. Пусть  . Выделим в
. Выделим в  все слагаемые, содержащие
все слагаемые, содержащие  :
:




В последнем представлении первое слагаемое представляет собой квадрат линейной формы по переменным  ; все оставшиеся слагаемые не зависят от
; все оставшиеся слагаемые не зависят от  , т.е. составляют квадратичную форму от переменных
, т.е. составляют квадратичную форму от переменных  . Таким образом, исходная задача для формы
. Таким образом, исходная задача для формы  переменных оказывается сведенной к случаю формы
переменных оказывается сведенной к случаю формы  -й переменной; последняя преобразуется по аналогичному принципу.
-й переменной; последняя преобразуется по аналогичному принципу.
2. Если  , но
, но  , т.е. при хотя бы одном квадрате переменной коэффициент отличен от нуля. Алгоритм модифицируется таким образом, что выделение полного квадрата начинается с переменной
, т.е. при хотя бы одном квадрате переменной коэффициент отличен от нуля. Алгоритм модифицируется таким образом, что выделение полного квадрата начинается с переменной  вместо
вместо  — первая ничем не лучше (и не хуже)
— первая ничем не лучше (и не хуже)  -й!
-й!
3. Совсем исключительный случай: квадраты переменных вообще отсутствуют, т.е. 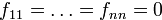 . Выбираем один из ненулевых коэффициентов при смешанных произведениях переменных: пусть
. Выбираем один из ненулевых коэффициентов при смешанных произведениях переменных: пусть  . Представляем
. Представляем  и заменяем все вхождения переменной
и заменяем все вхождения переменной  на
на  при вспомогательной переменной
при вспомогательной переменной  . В новой квадратичной форме уже присутствует квадрат переменной
. В новой квадратичной форме уже присутствует квадрат переменной  с ненулевым коэффициентом. Тем самым этот случай сводится к предыдущему. После приведения новой формы к сумме квадратов возвращаемся к «старой» переменной
с ненулевым коэффициентом. Тем самым этот случай сводится к предыдущему. После приведения новой формы к сумме квадратов возвращаемся к «старой» переменной  .
.
40)
Прямая — одно из основных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.