Условие, при котором две прямые лежат в одной плоскости

Пусть прямые L₁ и L₂ заданы каноническими уравнениями

Их направляющие векторы соответственно и (см. рис. 79).

Прямая L₁ проходит через точку радиус-вектор которой обозначим через ; прямая L₂ проходит через точку 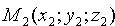, радиус-вектор которой обозначим через . Тогда

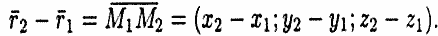
Прямые L₁ и L₂ лежат в одной плоскости, если векторы , и компланарны. Условием компланарности векторов явля­тся равенство нулю их смешанного произведения: , т. е.

При выполнении этого условия прямые L₁ и L₂ лежат в одной плоско­сти, то есть либо пересекаются, если , либо параллельны, если .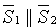

45)

Взаимное расположение нескольких прямых на плоскости

Две прямые, заданные уравнениями

или

пересекаются в точке

Угол γ ₁₂ между пересекающимися прямыми определяется формулой

При этом под γ ₁₂ понимается угол, на который надо повернуть первую прямую (заданную параметрами A ₁, B ₁, C ₁, k ₁ и b ₁) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.

Эти прямые параллельны, если A ₁ B ₂ − A ₂ B ₁ = 0 или k ₁ = k ₂, и перпендикулярны, если A ₁ A ₂ + B ₁ B ₂ = 0 или .

Любую прямую, параллельную A ₁ x + B ₁ y + C ₁ = 0, можно выразить уравнением A ₁ x + B ₁ y + C = 0. При этом расстояние между ними будет равно

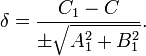
Если знак перед радикалом противоположен C ₁, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.

Для того, чтобы три прямые

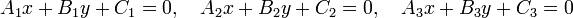
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие

Если и , то прямые 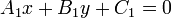и перпендикулярны.