
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Диверсификация как способ снижения риска
|
|
Не клади яйца в одну корзину.
Народная мудрость
Диверсификация заключается в формировании инвестиционного портфеля, который обеспечивает заданную доходность при минимальном риске или заданный риск при максимальной доходности. Формирование портфеля (portfolio construction) представляет собой процесс:
1) определения конкретных активов для вложения средств;
2) распределение инвестируемого капитала между активами.
Портфель описывается вектором
Χ = │ х 1, х 2, …, хn │, 
 ,
,
где  - доля исходящего капитала, инвестируемая в і -й актив;
- доля исходящего капитала, инвестируемая в і -й актив;
 - капитал, инвестируемый в і -й актив;
- капитал, инвестируемый в і -й актив;
 – суммарный инвестируемый капитал.
– суммарный инвестируемый капитал.
Для портфеля из двух активов х 1 + х 2 = 1, множество допустимых портфелей изобразится прямой на двумерной плоскости (рис.2.2).

Рис.2.2. Множество допустимых портфелей из двух активов
Если считать, что все хі  (инвестор по каждому активу находится в длинной (long) позиции, то множество допустимых портфелей соответствует отрезку этой прямой. Длинная позиция – это обычная покупка актива с намерением его последующей продажи (закрытие позиции). Портфель данного вида называется стандартным.
(инвестор по каждому активу находится в длинной (long) позиции, то множество допустимых портфелей соответствует отрезку этой прямой. Длинная позиция – это обычная покупка актива с намерением его последующей продажи (закрытие позиции). Портфель данного вида называется стандартным.
Отрицательное значение хі соответствует сделке, которая называется короткой продажей (short sale). В этом случае инвестор берет данный актив взаймы у другого инвестора (кредитора) и, рассчитывая на понижение стоимости этого актива, сразу же его продает, а впоследствии покупает этот актив на рынке по сниженной цене и возвращает его своему кредитору. При этом он обязан выплатить кредитору текущий доход по активу за время сделки и некоторый процент за предоставление кредита. Одновременно инвестор осуществив короткую продажу, может купить на вырученные деньги другие активы.
При трех активах множество допустимых стандартных портфелей представляет собой равносторонний треугольник с вершинами в единичных точках (рис.2.3).

Рис.2.3. Множество допустимых стандартных портфелей из трех активов
Любая точка этого треугольника соответствует конкретному портфелю
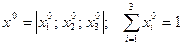 .
.
Множество допустимых портфелей из n- активов соответствует гиперплоскости, проходящей через единичные точки.
Доходность і -го  актива
актива  за конкретный период t равна
за конкретный период t равна
 ,
,
где Полный доход за период = Текущий доход за период + Прирост стоимости актива;
Прирост стоимости актива = Конечная стоимость актива - Начальная стоимость актива.
Доходность портфеля rp за период t определяется по формуле
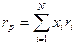 . (2.30)
. (2.30)
Как правило, доходность выражают в процентах.
Пример. Инвестор сформировал портфель из четырех активов, стоимость которых равна с 1 = 2 млн. грн.; с 2 = 10 млн. грн.; с 3 = 4 млн. грн.; с 4 = 4 млн. грн., а доходность активов r 1 = 30%; r 2 = 8%; r 3 = 10%; r 4 = 15%. Определить доходность портфеля.
Решение. В соответствии с выражением (2.30) имеем:
 .
.
Поскольку, как правило, ri – случайные величины, то доходность портфеля также является случайной величиной, которую оценивают математическим ожиданием  и дисперсией доходности портфеля
и дисперсией доходности портфеля  .
.
Используя свойства математического ожидания и дисперсии, получаем:
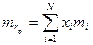 , (2.31)
, (2.31)
где  – математическое ожидание доходности і- го актива;
– математическое ожидание доходности і- го актива;
 , (2.32)
, (2.32)
где 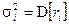 – дисперсия доходности і- го актива;
– дисперсия доходности і- го актива;
r ij – коэффициент корреляции между i- м и j -м активами.
Суть диверсификации – это разделение риска по принципу: “Не держи деньги в одном кармане” или, что то же самое, “Не клади яйца в одну корзину”, поскольку вероятность одновременного свершения нескольких нежелательных событий меньше, чем вероятность свершения одного из них. Продемонстрируем эффект диверсификации для случая, когда активы некоррелированы (r ij = 0).
Пусть  и
и  , а
, а  , тогда ожидаемая доходность портфеля
, тогда ожидаемая доходность портфеля
 ; (2.33)
; (2.33)
 . (2.34)
. (2.34)
Таким образом, при увеличении числа N активов в портфеле к ¥, получаем, что  стремится к нулю (2.34).
стремится к нулю (2.34).
В теории портфеля инвестиционный риск R определяется как изменчивость доходности, которая измеряется её дисперсией  , или среднеквадратическим отклонением
, или среднеквадратическим отклонением  .
.
Итак, инвестиционный риск в теории современного портфеля [18 ]
 . (2.35)
. (2.35)
Основные недостатки выбора дисперсии в качестве меры риска указывались выше.
Пример. Имеются два актива с m 1 = 10%, m 2 = 20%; s1 = 20%, s2 = 30% и r12 = -0, 5. Требуется найти множество оценок допустимых портфелей mp и s p.
Решение. Задавая значение х 1 от 0 до 1 (х 2=1– х 1), рассчитаем m p и sp по формуле
 ; (2.36)
; (2.36)
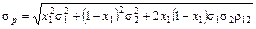 . (2.37)
. (2.37)
Расчетные данные сведем в следующую таблицу:
| Портфель, № | Доля капитала, вложенного в первый актив, x 1 | Доля капитала, вложенного во второй актив, x 2 | mp, % | s p, % |
| ¾ | ¼ | 12, 5 | ||
| ½ | ½ | 13, 2 | ||
| ¼ | ¾ | 17, 5 | 20, 2 | |
График оценок портфеля приведен на рис. 2.4.
Под эффективным (Парето-оптимальным) понимается портфель, имеющий максимальную ожидаемую доходность среди всех портфелей с данным уровнем риска. Таким образом, для каждого уровня риска имеется свой эффективный портфель (на рис. 2.4 – это портфели, соответствующие дуге 2 – 3 – 4 – 5). Портфели, соответствующие дуге 1 – 2 не являются эффективными.
При числе входящих в портфель активов больше двух множество оценок допустимых портфелей имеет вид представленный на рис. 2.5.

Рис. 2.4. Множество оценок портфелей из двух активов

Рис. 2.5. Множество оценок допустимых портфелей при числе активов больше двух
Но и в этом случае эффективные портфели соответствуют только дуге АВ.
Диверсификация портфеля может устранить риск (дисперсию доходности портфеля) для случая, если бы все активы были некоррелированны. В реальности практически все активы (ценные бумаги), присутствующие на фондовых рынках, испытывают воздействие общеэкономических факторов. При этом их взаимная корреляция является вполне заметной величиной.
В общем случае, когда активы являются коррелированными, N -мерная система случайных доходностей активов описывается корреляционной матрицей
 ,
,
или матрицей коэффициентов корреляции
 .
.
Учитывая, что дисперсия суммы случайных величин равна сумме всех элементов их корреляционной матрицы, а
Kij = Kji; Kii =  , а также то, что в доходность портфеля доходность актива входит с коэффициентом x, получаем:
, а также то, что в доходность портфеля доходность актива входит с коэффициентом x, получаем:

Если 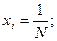
 ;
;  , то
, то

При N ® ¥, получаем  . Таким образом, взаимная корреляция не позволяет полностью устранить риск путем диверсификации, даже при N ® ¥. Она обуславливает так называемый недиверсифицируемый (рыночный или систематический) риск портфеля (рис 2.6).
. Таким образом, взаимная корреляция не позволяет полностью устранить риск путем диверсификации, даже при N ® ¥. Она обуславливает так называемый недиверсифицируемый (рыночный или систематический) риск портфеля (рис 2.6).

Рис. 2.6. Зависимость риска портфеля s p от числа активов N
Таким образом, общий риск (ОР) портфеля равен сумме недиверсифицируемого (НДР) и диверсифицируемого (ДР), который называется также нерыночным или несистематическим риском:
 .
.
Опыт показывает, что достаточно правильно отобрать
8 – 15 активов для того, чтобы практически устранить диверсифицируемый риск и, следовательно, уменьшить общий риск портфеля.
2.4. Коэффициент чувствительности “бета”
Для оценки доходности ценной бумаги используется рыночная модель (marker model) вида [18]
 , (2.38)
, (2.38)
где rj – доходность j -й ценной бумаги за данный период;
rІ – доходность на рыночный индекс за этот же период, определяемая средней рыночной доходностью всех акций, по которым вычисляется соответствующий рыночный индекс;
α j – коэффициент смещения “альфа”;
β j – коэффициент чувствительности “бета”;
ε j – случайная погрешность.
Коэффициент чувствительности β вычисляется по формуле
 ,
,
где КjI = σ j σ I ρ jI – корреляционный момент между доходностью j -й акции и доходностью на рыночный индекс I;
 – дисперсия доходности на рыночный индекс I;
– дисперсия доходности на рыночный индекс I;
σ j – среднеквадратическое отклонение доходности j -й акции;
ρ jI – коэффициент корреляции между доходностью j -й акции и доходностью на рыночный индекс I.
Расчетом коэффициента чувствительности β занимаются консалтинговые компании. При этом в качестве ρ jI , σ j, σ I берутся их оценки по выборке за определенный временной промежуток.
Если коэффициент β j для конкретной акции равен 1, 4, а фондовый индекс Доу-Джонса повысился на 20 пунктов, то относительно данной акции он возрастет на 20 ´ β j =
= 20 ´ 1, 4= 28 пунктов. Акции с коэффициентом β, больше единицы, обладают большей изменчивостью, чем рыночный индекс, и носят название “агрессивные” акции (aggressive stocks). И, наоборот, акции с β < 1обладают меньшей изменчивостью, чем рыночный индекс, и называются “оборонительными” акциями (defensive stocks).
Случайные погрешности ε j обусловлены неточностью рыночной модели и обладают следующими свойствами:
 .
.
В этом случае дисперсия доходности j -й ценной бумаги
 , (2.40)
, (2.40)
где  – дисперсия случайной погрешности ε.
– дисперсия случайной погрешности ε.
Доходность портфеля из N ценных бумаг
 (2.41)
(2.41)
где  – коэффициент смещения портфеля “альфа”;
– коэффициент смещения портфеля “альфа”;
 – коэффициент чувствительности портфеля “бета”;
– коэффициент чувствительности портфеля “бета”;
 – случайная ошибка доходности портфеля.
– случайная ошибка доходности портфеля.
Пример. Индекс Доу-Джонса на фондовом рынке уменьшился на 40 пунктов. Как изменится индекс доходности портфеля, имеющего следующие данные:
 ;
; 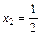 ;
;  ;
;  ;
;  ;
; 
Решение. Определяем коэффициент чувствительности портфеля
 .
.
Тогда индекс доходности портфеля уменьшится на  пункта.
пункта.
Из выражения для случайной доходности портфеля (2.41), с учетом свойств дисперсии, получаем выражение для дисперсии портфеля:
 . (2.42)
. (2.42)
Уравнение (2.42) также показывает, что общий риск портфеля (дисперсия доходности) состоит из двух компонент: недиверсифицированного риска  и диверсифицированного риска
и диверсифицированного риска 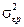 .
.
Для некоррелированных ценных бумаг
 . (2.43)
. (2.43)
Если предположить, что во все ценные бумаги инвестирована одинаковая сумма денег  , то уровень собственного риска
, то уровень собственного риска
 . (2.44)
. (2.44)
Второй сомножитель в выражении (2.44) является среднеарифметическим значением рисков ценных бумаг, входящих в портфель. Очевидно, что при  . Этот вывод переносится и на случай, когда весовые коэффициенты xi не равны между собой.
. Этот вывод переносится и на случай, когда весовые коэффициенты xi не равны между собой.