Решение. Так как m1 = m2, то для более детальной оценки степени риска принимаемого решения учтем дисперсии ожидаемого дохода:

m ₁ = 2× 0, 8 + 8× 0, 2 = 3, 2 млн. грн.

m ₂ = 4× 0, 8 + 0× 0.2 = 3, 2 млн. грн.

Так как m ₁ = m ₂, то для более детальной оценки степени риска принимаемого решения учтем дисперсии ожидаемого дохода:

.

Так как , то менее рискованным является второй проект.

В тех случаях, когда известен закон распределения случайной величины Х, характеризующей доходность, можно получить точную оценку риска, как вероятность нежелательного события.

В соответствии с определением функции распределения F (x) вероятность Р того, что случайная величина Х будет меньше любого заданного значения а равна значению функции распределения в точке а:

. (2.11)

Вероятность появления случайной величины в интервале [ a; b ] равна приращению функции распределения на этом интервале:

. (2.12)

Пример. Ожидаемый доход Х от инвестиций является случайной величиной, равномерно распределенной в интервале [0; 1] млн. грн.. Если доход будет меньше 100 тыс. грн., инвестор обанкротится. Оценить риск банкротства.

Решение. В данном случае риск R банкротства равен вероятности того, что доход Х будет меньше 100 тыс. грн. В соответствии с (2.11) имеем:

.

Для случайной величины, равномерно распределенной в интервале [0; 1000] тыс. грн., функция распределения имеет вид

График функции распределения F (x) показан на рис. 2.1.

Рис. 2.1. График функции распределения F (x) равномерно распределённой случайной величины

Риск банкротства R = F (100 тыс. грн.) = 0, 1.

Если известна плотность распределения f (x) непрерывной случайной величины Х, то из определения f (x) следует, что вероятность Р того, что случайная величина Х будет меньше любого заданного значения а, равна интегралу в пределах от – ¥ до а от плотности распределения:

. (2.13)

Вероятность того, что непрерывная случайная величина Х примет какое-нибудь значение из интервала [ a; b ],

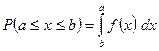. (2.14)

На практике широкое распространение получил гауссов закон распределения случайной величины Х:

. (2.15)

Объяснение этому даётся центральной предельной теоремой Ляпунова: если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на сумму ничтожно мало, то Х имеет распределение, близкое к гауссовому.

Для гауссова закона распределения, вероятность того, что случайная величина Х лежит в интервале [ а; b ] определяется соотношением

, (2.16)

где 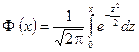– табулированная функция Лапласа.

Пример. Доход компании, состоящей из 100 различных независимых предприятий, приносящих примерно одинаковые доходы, является случайной величиной Х со следующими характеристиками: m_x = 300 млн. грн., s _x = 100 млн. грн. Банкротство компании произойдет, если полученный доход будет меньше 200 млн. грн. Оценить риск банкротства.

Решение. В данном случае величина риска будет определяться вероятностью того, что доход компании будет меньше 200 млн. грн.

Так как доход компании складывается из большого числа (100) доходов независимых предприятий, то его можно считать распределенным по закону Гаусса.

Найдем вероятность того, что доход компании лежит в пределах от 200 млн. грн. до ¥.

.

Используя таблицы функций Лапласа и учитывая, что
Ф(– а) = – Ф(а); Ф(¥) = 0, 5, находим

.

Тогда вероятность банкротства

.

Для гауссового закона вероятность

.

Другими словами, вероятность того, что абсолютная величина отклонения дохода от его математического ожидания превысит утроенное среднеквадратичное отклонение, очень мала, а именно равна 0, 0027. Это означает, что лишь в 0, 27% случаев это может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными (правило трех сигм).

В некоторых случаях решение принимается по степени риска, оцениваемом по коэффициенту вариации

, (2.17)

где – среднеквадратичное отклонение случайного ожидаемого дохода Х. При этом тот вариант действий считается предпочтительным, для которого коэффициент вариации меньше.

Коэффициент вариации является безразмерной величиной, поэтому пригоден для сравнения вариантов, характеризующихся различной размерностью.

Вместе с тем коэффициент вариации, как и любой другой мультипликативный показатель, имеет существенный недостаток: его можно обоснованно использовать лишь в тех случаях, когда отличаются друг от друга незначительно. Действительно, если, например, для одного варианта , , а для другого варианта и , то получаем, что

,

т.е. два варианта по коэффициенту вариации оказываются равнозначными. В то же время, ожидаемый доход в первом случае в 10000 раз больше ожидаемого дохода во втором случае.

Рассмотрим другие исходные данные:

, , а , .

Тогда

.

В этом случае, с позиции минимизации риска следует отдать предпочтение второму проекту.

Относительный риск определяется, как величина возможных убытков (потерь), отнесенной, например, к имуществу предпринимателя или к общим затратам ресурсов на данный вид предпринимательской деятельности. Коэффициент вариации, по существу, также является относительным риском.

Банками и финансовыми компаниями используется для оценки риска коэффициент Кука:

.

Вместе с тем надо понимать, что предприниматель вряд ли бы стал что бы то ни было предпринимать, если бы речь шла о максимально достижимой абсолютной прибыли в один доллар даже при доходности 100%.

Соотношение полезностей различных решений будет зависеть не столько от доходности инвестиций в процентом выражении, сколько от абсолютной величины стоимостных показателей. Если речь идет о выборе между двумя проектами инвестиций со ставками доходности 20% и 10% соответственно, в случае, когда реально выбираются проекты между абсолютными доходами 2 доллара и 1 доллар – оба проекта практически эквивалентны. Если же доход в абсолютном исчислении может составить 2 млн. долларов или 1 млн. долларов – различие становится существенным.