
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка риска
|
|
Если факторы, определяющие риск, являются случайными, то величина риска определяется или случайным событием, или случайной величиной, или функцией от случайных аргументов и полностью характеризуется в общем случае своим законом распределения: рядом распределения для дискретной случайной величины и плотностью распределения для непрерывной случайной величины. На практике риск, как случайная величина, оценивается числовыми характеристиками случайных событий или случайных величин. При этом в зависимости от вида риска и имеющихся исходных данных величина риска оценивается различным образом. Если риск определяется случайным событием, то его характеризуют соответствующей вероятностью.
Например, в страховании величину риска R определяют как вероятность p н появления нежелаемых событий (последствий):
 . (2.1)
. (2.1)
При этом  , где
, где  – частота появления нежелаемых событий, вычисляемая по статистическим данным.
– частота появления нежелаемых событий, вычисляемая по статистическим данным.
Например, в табл. 2.1 приведены данные о частоте летальных исходов у людей в зависимости от различных причин [10].
Таблица 2.1
| Причины гибели | Данные на 10 млн. чел. в год |
| Аварии автомашин | |
| Пожары и взрывы | |
| Водоемы | |
| Обращение с механизмами | |
| Автотранспорт | |
| Электричество | |
| Молнии | 5, 5 |
| Общественный транспорт | 0, 45 |
| Радиоактивное излучение | 0, 05 |
Если из 10 млн. человек в год погибнет в авиакатастрофах 75 человек, то вероятность того, что клиент страховой компании в течение года погибает от авиакатастрофы
 .
.
Табл. 2.1 можно использовать для обоснования оправданного риска, используя метод аналогий. Например, допустимый основной риск
 ,
,
соответствующий гибели в год 100 человек из 10 млн.
(10–5 чел/год), может быть рекомендован как допустимый при проектировании и эксплуатации технических средств. Эту величину не следует принимать как оправданный предел; она должна служить лишь основой относительной шкалы принимаемых решений.
Для летального риска принимают значения оправданного 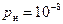 и неоправданного риска
и неоправданного риска  на человека в год; эти значения выглядят, в соответствии с табл. 2.1, разумными.
на человека в год; эти значения выглядят, в соответствии с табл. 2.1, разумными.
Если речь идет исключительно о риске материальных потерь, метод аналогий при оценке риска не вызывает сомнений. В этом случае можно принимать решения, оценивая лишь экономический эффект.
Если величина риска R определена, то решение о данном проекте принимается, если она не превышает допустимый уровень риска R доп.
Для определения R доп может использоваться как метод аналогий, так и экспертный метод. Очевидно, что оценка R доп экспертами является субъективной, зависящей от многих факторов, в том числе психологических. Например, предприниматель создает предприятие не только из-за желания добиться финансового благосостояния, но из-за желания быть независимым. Такие люди чувствуют дискомфорт при работе на “хозяина”, поэтому они принимают большой уровень допустимого риска. Очень богатые люди, напротив, не очень хотят рисковать своими деньгами. Их отношение к риску можно характеризовать такой фразой: “Я так долго добивался, чтобы заработать эти деньги, поэтому не собираюсь терять их в рискованных проектах”. Богатые становятся очень бережливыми и согласны на небольшую прибыль от безрисковых вкладов, которые не превышают 12% годовых. Но и излишняя осторожность не спасает от риска, избавиться от которого полностью невозможно.
Простая методика определения риска имеется и при использовании данных краткосрочного прогноза. Если вероятность прогноза равна p, то в качестве риска берут величину
 . (2.2)
. (2.2)
В общем случае риск определяется рядом последствий и вероятностями этих последствий, т.е. связан со случайной величиной, имеющей свой ряд распределения:
 ,
,
где xi – значение дохода, а pi – соответствующая этому значению вероятность, или (для непрерывной случайной величины) плотность распределения f (x), причем
 , а
, а  .
.
В соответствии с гипотезой ожидаемой полезности, человек выбирает решение, при котором величина ожидаемой полезности максимальна. Поэтому степень риска принимаемых решений связана с математическим ожиданием случайной величины Х:
 (2.3)
(2.3)
для дискретной случайной величины и
 (2.4)
(2.4)
для непрерывной случайной величины.
Пример. Фирма начинает выпускать автомобили. новой марки. В силу недостаточно изученного рынка сбыта во время маркетинговых исследований возможны три варианта спроса на продукцию. Прибыль при этом имеет следующий ряд распределения:
 .
.
Знак «–» означает, что фирма при таком исходе терпит убытки. Найти величину ожидаемой прибыли.
Решение. В соответствии с (2.3) имеем:
 = 7 ´ 0, 2 + 2 ´ 0, 6 – 5 ´ 0, 2 = 1, 6 млрд. грн.
= 7 ´ 0, 2 + 2 ´ 0, 6 – 5 ´ 0, 2 = 1, 6 млрд. грн.
В тех случаях, когда прибыль  является функцией от другой случайной величины Х с известным законом распределения
является функцией от другой случайной величины Х с известным законом распределения
 (2.5)
(2.5)
для дискретной случайной величины Х;
 (2.6)
(2.6)
для непрерывной случайной величины Х, где pxi – вероятность того, что случайная величина Х примет значение хi; f (x) – плотность распределения случайной величины Х.
Пример. Фирма по строительству коттеджей получает прибыль С, зависящую от количества полученных заказов Х следующим образом:
 ,
,
где k – постоянный коэффициент, имеющий размерность дохода.
Случайная величина Х имеет следующий ряд распределения:
 .
.
Найти величину ожидаемого дохода.
Решение. В соответствии с (2.5) получаем:

Если (X, Y) – система дискретных случайных величин (например, Х – величина спроса на выпускаемую продукцию; Y – цена на закупаемый для производства материал), распределение которой характеризуется матрицей распределения:

где  – вероятность того, что случайная величина Х примет значение хi и одновременно с этим случайная величина Y примет значение yj.
– вероятность того, что случайная величина Х примет значение хi и одновременно с этим случайная величина Y примет значение yj.
В этом случае доход С есть функция случайных аргументов x и y:
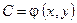 ,
,
а
 . (2.7)
. (2.7)
Если (x, y) – система непрерывных случайных величин с плотностью распределения f (x, y), то
 . (2.8)
. (2.8)
Пример. Акционер имеет акции двух взаимосвязанных по производственной деятельности компаний. На рынке могут возникнуть ситуации, при которых курсы акций Х и Y этих компаний характеризуются следующей матрицей распределения:

Найти величину математического ожидания дохода, если количество акций первого вида равно 100; другого – 50, а стоимость всех акций при покупке составляла 1000 грн.
Решение. В данном случае доход С = 100 х + 50 y – 1000 грн.. В соответствии с выражением (2.7) имеем:
 = 500´ 0, 2 + 1000´ 0, 1 +
= 500´ 0, 2 + 1000´ 0, 1 +
+1500´ 0, 1 + 1000´ 0, 1 + 1500´ 0, 2 + 2000´ 0, 3 = 1500.
Математическоеожидание – лишь одна характеристика случайной величины, которая определяет величину риска. Эта характеристика позволяет грубо оценить и другую характеристику риска, – вероятность нежелательного события. Для этого нужно использовать неравенство Маркова.
Неравенство Маркова: если среди значений случайной величины X нет отрицательных, то вероятность P того, что она примет какое-нибудь значение, превосходящее положительное число a, не больше дроби mx / а, т. е.
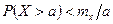 .
.
Пример. Среднесуточное потребление электроэнергии в населенном пункте равно mx = 20000 кВт/ч. Оценить вероятность того, что потребление электроэнергии в этом населённом пункте в течение данных суток превзойдет критическое значение, равное а = 60000 кВт/ч.
Решение. Используя неравенство Маркова, получаем оценку критического риска  .
.
Второй характеристикой случайной величины является дисперсия (часто именно эту характеристику и берут в качестве величины риска):
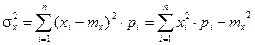 (2.9)
(2.9)
для дискретной случайной величины Х и
 (2.10)
(2.10)
для непрерывной случайной величины Х, где mx – математическое ожидание этой случайной величины.
Поскольку дисперсия характеризует степень рассеяния возможных значений случайной величины относительно её среднего значения, то считается, что чем меньше будет рассеяние ожидаемого дохода, тем лучше это будет для предпринимателя. Основными недостатками выбора дисперсии в качестве меры риска являются:
- Дисперсия учитывает отклонения в обе стороны относительно математического ожидания. Инвестор же не оценивает превышение доходности над ожидаемой как нежелательный результат. Наоборот, такой результат может только приветствоваться.
- Вероятность нежелательного события (например, банкротство; доход меньше допустимого и др.) зависит не только от дисперсии, но и от математического ожидания. Таким образом, риск является многомерной характеристикой.
Тем не менее, использование дисперсии в качестве меры риска показало свою эффективность в большинстве практических случаев.
Пример. Имеется два варианта производства и реализации товаров. По данным отдела маркетинга, который провел исследования рынка, ожидаемые доходы зависят от вероятности экономической ситуации (табл. 2.2).
Таблица 2.2
| Варианты производства и реализации товаров | Доход; экономическая ситуация | |
| р 1 = 0, 8 | р 2 = 0, 2 | |
| Первый | 2 млн. грн. | 8 млн. грн. |
| Второй | 4 млн. грн. |
Необходимо оценить степень риска и принять решение относительно выпуска одного из двух видов товаров.