
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Использование неравенства Чебышева для оценки риска
|
|
Как уже отмечалось, математическое ожидание и дисперсия являются двумя показателями, определяющими степень риска, но если воспользоваться неравенством Чебышева, можно получить один показатель (вероятность нежелательного события), зависящий от этих двух даже в том случае, когда неизвестен закон распределения случайной величины.
Неравенство Чебышева. Если случайная величина Х имеет конечную дисперсию  и математическое ожидание mx, то вероятность Р того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине будет меньше любого положительного числа e > 0, определяется неравенством
и математическое ожидание mx, то вероятность Р того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине будет меньше любого положительного числа e > 0, определяется неравенством
 . (2.18)
. (2.18)
Вторая форма неравенства Чебышева имеет вид
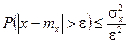 . (2.19)
. (2.19)
Пусть инвестиции осуществляются за счет кредита, взятого под залог недвижимости под процентную ставку rk. Оценим риск того, что инвестор не сможет вернуть свой долг и потеряет недвижимость (риск банкротства).
В данном случае риск R будет оцениваться вероятностью Р нежелательного события, что ожидаемая доходность инвестиций Х окажется меньше rk:
X < rk. (2.20)
Неравенство (2.20) можно записать в следующем виде:
 . (2.21)
. (2.21)
Тогда вероятность события
 . (2.22)
. (2.22)
Используя неравенство Чебышева и обозначая 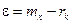 , получаем
, получаем
 . (2.23)
. (2.23)
Таким образом, степень риска
 . (2.24)
. (2.24)
Если, например, инвестор хочет, чтобы риск банкротства был не больше, чем 
 , то для этого необходимо выполнить условие
, то для этого необходимо выполнить условие

или
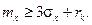 (2.25)
(2.25)
Во многих случаях допустимый риск имеет меньшую величину, например р доп = 0, 001.
В этом случае
 ,
,
или
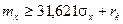 .
.
Пример. Предприниматель берет кредит под 10% годовых для реализации инновационного проекта. При этом эксперты оценивают, что риск (среднее квадратическое отклонение), связанный с колебанием ожидаемой доходности проекта  , равен 5%. Необходимо оценить уровень ожидаемого доходности
, равен 5%. Необходимо оценить уровень ожидаемого доходности  , чтобы избежать банкротства с вероятностью
, чтобы избежать банкротства с вероятностью  .
.
Решение. Имеем  . Используем формулу (2.25), получаем
. Используем формулу (2.25), получаем
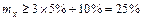 ,
,
т.е. уровень ожидаемой доходности должен быть не меньше, чем 25%.
Рассмотрим еще одну ситуацию, когда инвестор вкладывает в обычные акции лишь часть своего капитала, оставляя некоторую часть на сохранность под практически безрисковую процентную ставку наращивания  . Какая будет при этом величина риска (вероятность банкротства)?
. Какая будет при этом величина риска (вероятность банкротства)?
Пусть А – капитал инвестора, тогда х 0 А – часть, которая вкладывается в практически безрисковый актив с процентной ставкой  .
.
Очевидно, что банкротство будет в случае, когда
 , (2.26)
, (2.26)
где  – процентная ставка обычных акций (очевидно, что для банкротства
– процентная ставка обычных акций (очевидно, что для банкротства  должна быть отрицательной).
должна быть отрицательной).
Из выражения (2.26), получаем, что банкротство будет в том случае, когда
 . (2.27)
. (2.27)
Используя неравенство Чебышева, определим уровень ожидаемого дохода от обычных акций, при котором вероятность банкротства будет меньше  . Считая, что
. Считая, что  есть случайная величина Х, имеем:
есть случайная величина Х, имеем:

Отсюда
 . (2.28)
. (2.28)
Сравнивая выражение (2.28) и (2.25), видим, что игра на бирже на собственный капитал существенно менее рискованна. Даже если вложить весь собственный капитал в обычные акции (х 0 = 0), то уровень ожидаемой доходности от акций, позволяющий избежать банкротства с вероятностью  , должен быть не меньше
, должен быть не меньше
 . (2.29)
. (2.29)
Пример. Инвестор вкладывает половину своего капитала  в безрисковые ценные бумаги, доходность
в безрисковые ценные бумаги, доходность  от которых составляет 30%. Вторую половину денег он собирается вложить в рискованный проект. Среднеквадратичное отклонение
от которых составляет 30%. Вторую половину денег он собирается вложить в рискованный проект. Среднеквадратичное отклонение  доходности от этого проекта равно 100(%.) Инвестор хотел бы, чтобы вероятность банкротства была бы для него не больше
доходности от этого проекта равно 100(%.) Инвестор хотел бы, чтобы вероятность банкротства была бы для него не больше  . Какой для этого должна быть ожидаемая доходность от инвестиций?
. Какой для этого должна быть ожидаемая доходность от инвестиций?
Решение. Используя выражение (2.28), получаем
 .
.
Следовательно, ожидаемая доходность от инвестиций должна быть не менее 70%.
Пример. При производстве товаров на экспорт, производитель хотел бы, чтобы риск банкротства был бы не больше  . В производстве вкладывают весь собственный капитал. Ожидаемый уровень доходности
. В производстве вкладывают весь собственный капитал. Ожидаемый уровень доходности  составляет 10%.
составляет 10%.
Определить, каким должно быть среднеквадратичное отклонение доходности  .
.
Решение. Дано: х 0 = 0,  .
.
В соответствии с выражением (2.28) имеем
 .
.
Таким образом, среднеквадратичное отклонение должно быть не больше, чем 36, 7%.
Неравенство Чебышева дает более грубую оценку риска по сравнению с той, которую получают по известному закону распределения случайной величины Х, характеризующей доходность.