Оптимизация риска

Лучший из всех портфелей на эффективной границе называется оптимальным портфелем. Но выбор оптимального портфеля зависит от предпочтений инвестора при выборе между риском и доходностью. Эти предпочтения описываются при помощи функции полезности (критерия полезности).

Кривая безразличия определяет комбинации риска и ожидаемой доходности, дающей одинаковый уровень полезности (одно и то же значение критерия полезности).

На рис. 2.7 изображены множество оценок допустимых портфелей и кривые безразличия. Чем выше находится кривая безразличия, тем большей полезности L_i для инвестора она соответствует.

Оптимальный портфель соответствует точке касания N эффективной границы оценок портфеля и некоторой кривой безразличия (L ₂). Эта кривая соответствует максимальному значению полезности среди кривых, пересекающих допустимое множество оценок портфелей.

Рис. 2.7. Определение оптимального портфеля с помощью кривых безразличия

При линейной функции полезности

L = m_p - k s _p, (2.45)

где k – коэффициент, характеризующий отношение инвестора к риску. Чем больше k, тем круче кривые безразличия, тем меньше инвестор склонен к риску (рис. 2.8).

По существу, нахождение оптимального портфеля является двухкритериальной задачей.

Для нахождения портфеля из двух активов, имеющего минимальный риск, необходимо решить уравнение

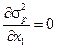. (2.46)

Так как 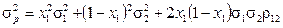, то

.

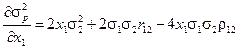Рис. 2.8. Нахождение оптимального портфеля при линейной кривой безразличия

Приравнивая значение этой производной нулю, получаем оптимальное значение х _{1 opt} , обеспечивающее минимальную дисперсию:

. (2.47)

При r₁₂ = 0;

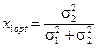. (2.48)

При r₁₂ = 1;.

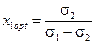. (2.49)

При r₁₂ = -1;

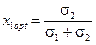. (2.50)

Пример. Найти портфель с минимальной дисперсией, если он состоит из двух активов с m ₁=5%; m ₂=10%; 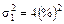; ; 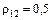и определить его характеристики.

Решение. В соответствии с (2.47) получаем

.

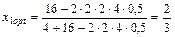Тогда .

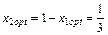Характеристики портфеля:

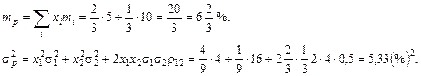
В общем случае нахождение оптимального портфеля по Марковицу (минимизация риска при заданном уровне ожидаемой доходности) является задачей квадратичного программирования, так как весовые коэффициенты х_i, входят в выражение для дисперсии в квадрате [18].