
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгебраические критерии устойчивости
|
|
Частотные динамические характеристики
Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Зная частотную характеристику элемента, можно определить реакцию элемента на гармоническое воздействие любой частоты, а также на сумму гармонических воздействий различной частоты. Частотные характеристики широко используются в теории и практике автоматического управления, так как реальные возмущения, действующие на автоматические системы, могут быть представлены как сумма гармонических сигналов.
Пусть на вход линейного элемента в момент времени t=0 подано гармоническое воздействие определенной частоты w
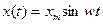
Через некоторое время, необходимое для протекания переходного процесса, элемент войдет в режим установившихся вынужденных колебаний, а выходная величина y(t) будет изменяться по гармоническому закону с той же частотой w, но с отличающейся амплитудой ym и со сдвигом 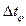 по оси времени
по оси времени
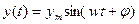
где 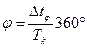 - фазовый сдвиг между входным и выходным сигналами;
- фазовый сдвиг между входным и выходным сигналами;
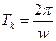 - период колебаний.
- период колебаний.
Повторяя такой эксперимент при фиксированном  для различных значений частоты (от 0 до
для различных значений частоты (от 0 до  ), можно установить, что амплитуда
), можно установить, что амплитуда  и фазовый сдвиг
и фазовый сдвиг 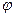 выходного сигнала конкретного элемента зависят от частоты воздействия.
выходного сигнала конкретного элемента зависят от частоты воздействия.
Подавая гармоническое воздействие на вход различных элементов, можно убедиться, что величины 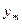 и
и 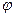 зависят также от типа и параметров элемента.
зависят также от типа и параметров элемента.
Так как амплитуда выходного сигнала зависит ещё от амплитуды входного сигнала, то целесообразно при описании передаточных свойств элементов рассматривать отношение амплитуд 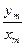 .
.
Зависимость отношения амплитуд выходного и входного сигнала от частоты называют амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А(w) (см. рис.а). Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой (ФЧХ) и обозначают j(w) (см. рис.б). Аналитические выражения А(w) и j(w) называют соответственно амплитудной и фазовой частотными функциями.
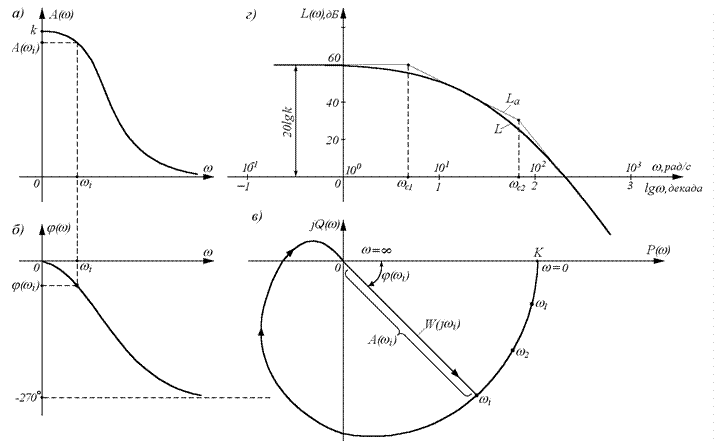
АЧХ показывает, как элемент пропускает сигналы различной частоты. Оценка пропускания производится по отношению амплитуд  в установившемся режиме. АЧХ имеет размерность, равную отношению размерности выходной величины к размерности входной. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах в установившемся режиме.
в установившемся режиме. АЧХ имеет размерность, равную отношению размерности выходной величины к размерности входной. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах в установившемся режиме.
Амплитудную и фазовую частотные характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ или АФХ). Амплитудно-фазовая частотная характеристикаW(jw) представляет собой функцию комплексного переменного jw, модуль которой равен А(w), а аргумент равен j(w). Каждому фиксированному значению частоты wi соответствует комплексное число W(jwi), которое на комплексной плоскости можно изобразить вектором, имеющим длину А(wi) и угол поворота j(wi) (см. рис.в). Отрицательные значения j(w), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси.
При изменении частоты от нуля до бесконечности вектор W(jw) поворачивается вокруг начала координат, при этом одновременно увеличивается или уменьшается длина вектора. Кривая, которую при этом опишет конец вектора, называемая годографом, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты.
Проекции вектора W(jw) на действительную и мнимую оси называют соответственно действительной и мнимой частотными характеристиками и обозначают
При этом, действительная частотная характеристика Р(w) – всегда четная функция частоты, а мнимая характеристика Q(w) – всегда нечетная функция.
Аналитическое выражение для АФЧХ конкретного элемента можно получить из его передаточной функции путем подстановки р=jw:
АФЧХ W(jw), как и любая комплексная величина, может быть представлена в показательной форме
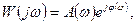
где А(w) – модуль АФЧХ, а j(w) – угол сдвига по фазе;
алгебраической
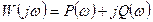
или тригонометрической
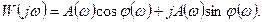
Связь между различными частотными функциями следующая:
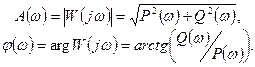
Выделение действительной и мнимой составляющих частотной передаточной функции 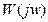 возможно с помощью следующих формул:
возможно с помощью следующих формул:
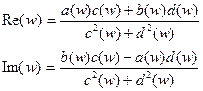
где 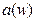 - действительная часть числителя функции
- действительная часть числителя функции 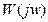
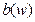 - мнимая часть числителя
- мнимая часть числителя
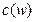 - действительная часть знаменателя
- действительная часть знаменателя
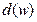 - мнимая часть знаменателя
- мнимая часть знаменателя
При практических расчетах автоматических систем удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков.
За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением wi и его десятикратным значением 10 wi. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1. При построении ЛЧХ по оси абсцисс откладывают логарифм частоты, а подписывают соответствующие значения частот. Ось ординат проводят через произвольную точку.
Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)
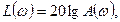
ординаты которой измеряют в логарифмических единицах – белах (Б) или децибелах (дБ).
При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс.
На рис.г показаны ЛАЧХ L(w) (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристика Lа(w) в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими и обозначают wс.
По виду частотных характеристик все элементы и системы делят на 2 группы: минимально-фазовые и неминимально-фазовые. Минимально-фазовые – такие, у которых все нули и полюса передаточной функции имеют отрицательные действительные части. Такие элементы дают минимальный фазовый сдвиг по сравнению с любыми другими элементами, имеющими такую же амплитудную характеристику, но у которой действительная часть хотя бы одного полюса или нуля положительна. Для примера, звенья  имеют одинаковые ЛАЧХ, но разные ЛФЧХ.
имеют одинаковые ЛАЧХ, но разные ЛФЧХ.
Алгебраические критерии устойчивости