Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частотные критерии устойчивости
|
|
На практике широкое распространение получили частотные критерии устойчивости: критерий Михайлова, критерий Найквиста. И тот, и другой критерии базируются на принципе комплексного аргумента.
Принцип аргумента. Рассмотрим уравнение:
,
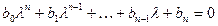здесь li – корни данного уравнения
.
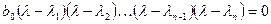Каждому корню li на комплексной плоскости соответствует некоторая точка. Если соединить точку с нулем, то можно говорить о векторе.
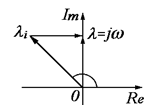Длина вектора равна модулю комплексного числа li, а угол, образуемый положительной действительной осью и вектором li, есть аргумент комплексного числа li.
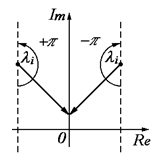Придадим l значение jw (l = jw). Считаем движение против часовой стрелки положительным, тогда для корней, находящихся в левой части комплексной плоскости при изменении частоты 
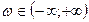, вектор (l-li) описывает угол + p.
Для корней, находящихся в правой полуплоскости, вектор (l-li) при изменении частоты 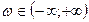опишет угол - p.
Считаем, что порядок системы п -ый, и m корней положительные, значит отрицательных – п-т. Тогда суммарный угол поворота всех векторов составит следующее выражение:
.
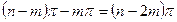