
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерий Найквиста
|
|
Критерий Найквиста был сформулирован в 1932 г. американским физиком X. Найквистом. В отличие от критериев Гурвица, Рауса и Михайлова, которые основаны на анализе характеристического уравнения системы, критерий Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутого контура системы.
В этом заключается существенное преимущество критерия, т.к. построение АФХ разомкнутого контура для большинства реальных систем оказывается проще, чем построение годографа Михайлова. Особенно упрощается это построение для одноконтурных систем, состоящих из типовых звеньев.
Имеется САУ:

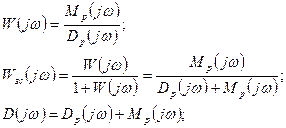
здесь Dp(jw) – частотное характеристическое уравнение разомкнутой системы.
Найквист в своем критерии рассматривает вспомогательную функцию, определяемую по формуле
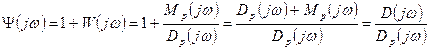
Примечание: Возьмем абстрактное комплексное число
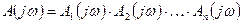 .
.
Модуль этого числа будет равен произведению модулей каждого из множителей, а аргумент этого числа – сумме каждого из слагаемых.
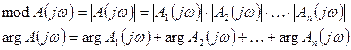
Причем
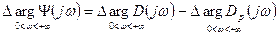 .
.
Рассмотрим два случая.
1. Система в разомкнутом состоянии устойчива, это значит по Михайлову:
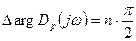 ,
,
где п – порядок разомкнутой системы.
Частотное характеристическое уравнение замкнутой системы также имеет порядок п, т.к. порядок числителя разомкнутой системы всегда меньше или равен порядку знаменателя разомкнутой системы (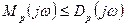 ).
).
Если система в замкнутом состоянии тоже устойчива, то угол одинаковый
 .
.
Рассмотрим изменения аргумента 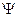 при изменении частоты от 0 до ¥:
при изменении частоты от 0 до ¥:
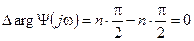
Система в замкнутом состоянии будет устойчива, если изменение аргумента функции  при изменении частоты от 0 до ¥ составит ноль. Это возможно только в том случае, когда годограф не охватывает точку начала координат (рис, а). Но если рассматривать годограф функции
при изменении частоты от 0 до ¥ составит ноль. Это возможно только в том случае, когда годограф не охватывает точку начала координат (рис, а). Но если рассматривать годограф функции  , то этому соответствует случай, когда не охватывается точка (-1; ј0) (рис б).
, то этому соответствует случай, когда не охватывается точка (-1; ј0) (рис б).

Критерий Найквиста для первого случая: замкнутая система будет устойчивой, если годограф разомкнутой системы не пересекает отрезок (-¥; -1], т.е. не охватывает критическую точку (-1; 0).
Употребленное в формулировке критерия Найквиста понятие охвата точки имеет некоторую неопределенность, из-за чего в случаях сложной формы кривой W(јω) могут возникнуть затруднения в суждении об устойчивости системы. Поэтому для суждения об устойчивости систем, имеющих АФЧХ сложной конфигурации, когда кривая АФЧХ пересекает действительную ось левее точки с координатами (-1; ј0) несколько раз, можно также использовать правило переходов, сформулированное советским ученым Я. 3. Цыпкиным: АФЧХ не охватывает точку (-1; ј0), если при возрастании w разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФЧХ через ось абсцисс слева от точки (-1; ј 0) равна нулю.
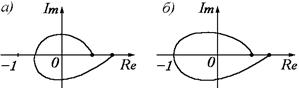 |
На рисунке а) изображен годограф системы, устойчивой в замкнутом состоянии, а на б) – системы, находящейся на границе устойчивости.
Система находится на границе устойчивости, если годограф, соответствующий амплитудно-фазовой характеристики разомкнутой системы хотя бы один раз пересечет точку [-1; 0].
2. Разомкнутая система неустойчива.
Разомкнутая система неустойчива, это значит, что изменение аргумента представляется формулой:
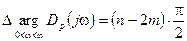 ,
,
где m – количество корней характеристического уравнения разомкнутой системы, находящихся в правой полуплоскости.
У замкнутой системы изменение аргумента при изменении частоты от 0 до ¥:
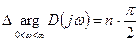 для устойчивой системы
для устойчивой системы
Изменение аргумента вспомогательной функции составит:
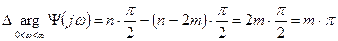 .
.
Тогда критерий Найквиста звучит так:
если система неустойчива в разомкнутом состоянии и имеет m положительных корней характеристического уравнения, то система в замкнутом состоянии будет устойчива лишь в том случае, если годограф разомкнутой системы охватывает точку (-1; ј0) в положительном направлении m раз, или, используя правило переходов: разность между количеством положительных переходов и количеством отрицательных переходов отрезка 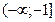 действительной оси будет равна
действительной оси будет равна  .
.
Объединяя два случая, можно дать следующее определение критерия Найквиста:
Система в замкнутом состоянии будет устойчива, если разность между числами положительных и отрицательных переходов годографа АФЧХ разомкнутой системы на отрезке 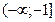 действительной оси будет равна
действительной оси будет равна  , где т – количество правых корней характеристического уравнения разомкнутой системы.
, где т – количество правых корней характеристического уравнения разомкнутой системы.
Если АФЧХ начинается или заканчивается на отрезке (-∞; -1), то считают, что характеристика совершает полперехода.
Примеры:
1. т = 2

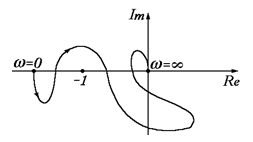 2. т = 2
2. т = 2