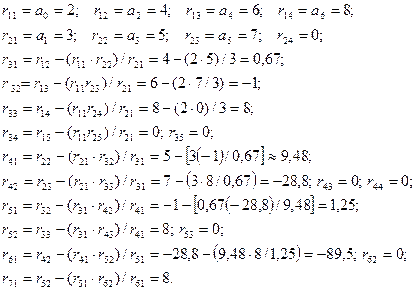Автоматическая система, описываемая характеристическим уравнением

,

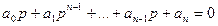устойчива, если при a₀ > 0 положительны все определители ∆ ₁, ∆ ₂,...∆ _п вида

Если хотя бы один из определителей, называемых определителями Гурвица, отрицателен, то система неустойчива. Если главный определитель ∆ _п =0, а все остальные определители положительны, то система находится на границе устойчивости.

Рассмотрим частные случаи критерия Гурвица для n =1; 2; 3; 4. Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить следующие условия.

1. Для уравнения первого порядка (n =1)

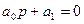
условие устойчивости: а₀ > 0 и ∆ ₁ = а₁ > 0, т.е. для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.

2. Для уравнения второго порядка (n =2)

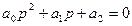
условие устойчивости:

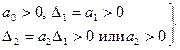
Т.о., и для системы второго порядка необходимое условие устойчивости (положительность коэффициентов) является одновременно и достаточным.

3. Для уравнения третьего порядка (n =3)

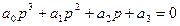
условие устойчивости:

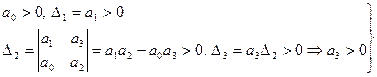
При n =3 для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля и произведение средних коэффициентов уравнения (а₁, а₂) было больше произведения крайних (а₀, а₃).

4. Для уравнения четвертого порядка (n =4)

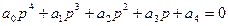
кроме положительности всех коэффициентов требуется выполнение условия

.

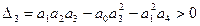При n =4 система будет устойчива при всех коэффициентах больших нуля и при

.

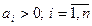Т.о., для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель

∆ _п-1 были положительными.

Критерий Рауса.

САУ будет устойчивой, если будут положительны все элементы первого столбца таблицы Рауса (включая а₀ и а₁).

,

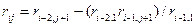где i – номер строки, j – номер столбца.

Если не все коэффициенты столбца положительны, то система неустойчива. При этом число перемен знака среди этих коэффициентов соответствует числу правых корней характеристического уравнения.

Таблица:

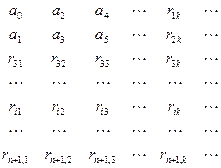
Пример:

Характеристическое уравнение: