
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рассмотрим характеристическое уравнение системы
|
|
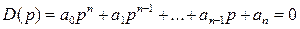
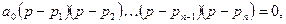
p=jw - придаем чисто мнимое значение.
Для того чтобы система была устойчивой, необходимо, чтобы суммарный угол поворота векторов р-рi составлял угол pn.
В характеристическом уравнении заменяем р на jw. Тогда получим функцию комплексного переменного:
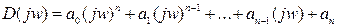
которую можно так же, как амплитудно-фазовую характеристику, представить в виде суммы действительной и мнимой частей:

Действительная часть Re(w) содержит только четные степени переменного w:
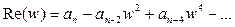
а мнимая часть Im(w)— только нечетные:
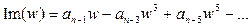
Действительная часть характеристического уравнения является функцией четной, а мнимая часть – нечетной.
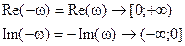
Поэтому достаточно ограничиться построением кривой, соответствующей характеристическому полиному для положительных частот. Тогда кривая, соответствующая отрицательным частотам является зеркальным отражением кривой для положительных частот относительно оси абсцисс.
Каждому фиксированному значению переменного w соответствует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости. Если теперь изменять параметр w от 0 до ¥, то конец вектора D(jw) опишет некоторую линию, которая называется характеристической кривой или годографом Михайлова. По виду этой кривой можно судить об устойчивости системы.