
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение движения имеет вид
|
|
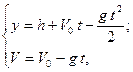
при t = τ, y = 0, тогда
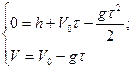
Все три варианта дают одинаковые уравнения движения при t = τ
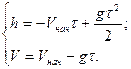
Для определения 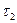 решим квадратное уравнение
решим квадратное уравнение
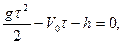
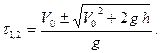
Корень 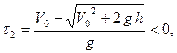 его не учитываем, так как он не имеет физического смысла.
его не учитываем, так как он не имеет физического смысла.
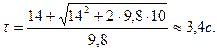
а) Можно найти максимальную высоту подъема камня, исходя из того, что дискриминант 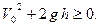
Тогда 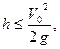 а максимальное значение
а максимальное значение
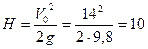 м;
м;
б) Найти время, по истечении которого камень находится в любой промежуточной точке своего пути.
При 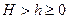 ,
, 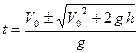 имеет два значения, так как в каждой точке камень бывает дважды за время движения.
имеет два значения, так как в каждой точке камень бывает дважды за время движения.
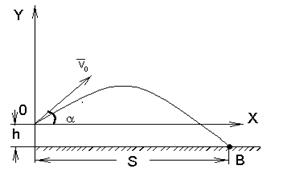
Задача 5. Камень брошен с высоты h =2, 1 м под углом a = 45˚ к горизонту и падает на землю на расстоянии S = 42 м (по горизонтали) от места бросания. Найти начальную скорость V 0 камня, время полета τ и максимальную высоту подъема над уровнем земли. Определить также радиусы кривизны траектории в верхней точке и в точке падения камня на землю.
 Дано: Решение
Дано: Решение
 h = 2, 1 м
h = 2, 1 м
a = 45˚
S = 42 м

V 0 -? τ -? H -?
R 1 и R 2 -?
Рис.1.6
Движение камня, происходящее по параболе, можно рассматривать как сумму двух независимых движений: равномерного движения по горизонтали (по оси Х) и равнопеременного по вертикали (по оси Y). Начало отсчета удобно выбрать в точке бросания. Ось Y направлена вертикально вверх.
Для движения камня по оси Х получаем 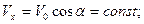
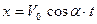 ; при t = τ x = S.
; при t = τ x = S.
Следовательно,
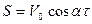 (1)
(1)
Для движения по оси OY
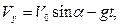 (2)
(2)
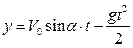 . (3)
. (3)
При t = τ, y = - h, поэтому
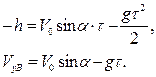 (4)
(4)
(5)
Решая совместно уравнения (1) и (4), находим τ и V 0:
1) τ = 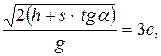
2) 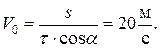
3) Высоту подъёма камня можно найти из условия H = h + ymax.
При 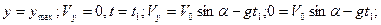
отсюда 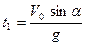 (
(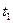 – время подъёма камня).
– время подъёма камня).
Подставив 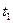 в уравнение (4), получим
в уравнение (4), получим 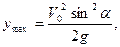 тогда
тогда
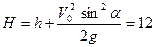 м.
м.
4) Для определения радиуса кривизны траектории в данной точке нужно определить по величине и направлению вектор полного ускорения. В верхней точке траектории 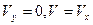 , следовательно, векторы ускорения и скорости взаимно перпендикулярны. Это значит, что aτ = 0, an = g. Зная ускорение и скорость, найдём радиус кривизны траектории в верхней точке.
, следовательно, векторы ускорения и скорости взаимно перпендикулярны. Это значит, что aτ = 0, an = g. Зная ускорение и скорость, найдём радиус кривизны траектории в верхней точке.
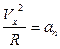 ;
; 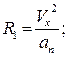
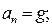 и
и 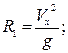


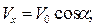
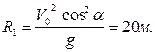
В конечной точке траектории синус угла β между векторами скорости и ускорения может быть выражен как показано на рис.1.7.
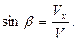

Разложим вектор полного ускорения на нормальное и тангенциальное, получим 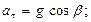
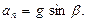
Радиус траектории в этой точке находится из соотношения 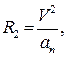 т.е.
т.е. 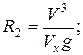
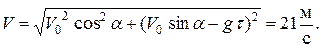
Тогда R 2 = 63 м.
Ответ: 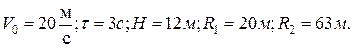
 Задача 6. Тело вращается вокруг неподвижной оси по закону φ = 10 + 20 t – 2 t 2 рад. Найти: 1) Угловую скорость, угловое ускорение и полное ускорение точки, находящейся на расстоянии R = 0, 1 м от оси вращения, для момента времени
Задача 6. Тело вращается вокруг неподвижной оси по закону φ = 10 + 20 t – 2 t 2 рад. Найти: 1) Угловую скорость, угловое ускорение и полное ускорение точки, находящейся на расстоянии R = 0, 1 м от оси вращения, для момента времени 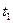 = 4 с (рис. 1.8). 2) Через сколько времени тело остановится? 3)Сколько оборотов сделает до остановки?
= 4 с (рис. 1.8). 2) Через сколько времени тело остановится? 3)Сколько оборотов сделает до остановки?
 Дано:
Дано:
φ = 10 + 20 t – 2 t 2 рад
R = 0, 1 м
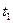 = 4 c
= 4 c
w = 0

 -? ε -? a -? t -? N -?
-? ε -? a -? t -? N -?
Рис. 1.8