Одноканальная система массового обслуживания с неограниченной очередью

Пусть СМО имеет один канал обслуживания, на который поступает простейший поток заявок с интенсивностью λ. Время обслуживания распределено по показательному закону с параметром μ. Если заявка поступает в СМО в момент занятости канала, то они становятся в очередь. Число мест в очереди не ограниченно. Следовательно, каждая заявка рано или поздно будет обслужена, т. е.

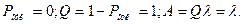(24)

Вычислим коэффициент загрузки СМО 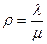. Предельное распределение вероятностей состояний данной СМО существует только при . Этот факт легко объяснить, если рассматривать данную СМО как предельный случай одноканальной СМО с ограниченной очередью при стремлении длины очереди к бесконечности. Тогда предельное распределение вероятностей состояний можно вычислить как придел при предельных вероятностей (22). При этом возникает бесконечный числовой ряд (см. 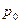), состоящий из членов геометрической прогрессии, который сходится, если знаменатель прогрессии меньше 1, т. е. , и имеет сумму .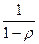

Таким образом, предельные вероятности состояний вычисляются по формулам:

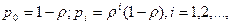(25)

где 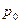– предельная вероятность того, что канал свободен;

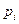– предельная вероятность того, что канал занят и 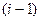заявка в очереди.

Переходя к пределу при из формул (23) и (25) получим показатель эффективности СМО с неограниченной очередью:

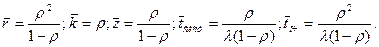(26)