Определение наличия тренда

Определим наличие тренда с помощью критерия серий, основанном на медиане выборки. Все расчеты приведены на рис.17-18. Поскольку первое неравенство (6) нарушается, то данный ряд имеет тренд

Определим наличие тренда с помощью проверки разностей средних уровней. Все расчеты приведены на рис. 19 - 20. Для этого исходный временной ряд разбиваем на две равные части по числу уровне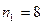й: и 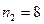(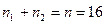). В каждой части вычисляем средние значения и проверяем равенство средних.

Проверка равенства средних значений осуществлена с помощью критерия Стьюдента и критерия Фишера [9], с использованием встроенных функций MS Excel. Поскольку гипотеза о равенстве средних не подтвердилось, то принимаем гипотезу о том, что данный ряд имеет тренд.

.

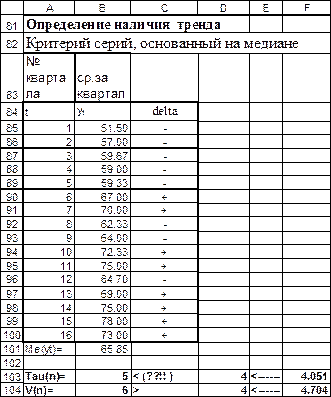
Рис. 17. Определение наличия тренда с помощью критерия серий, основанном на медиане выборки (режим отображения данных)

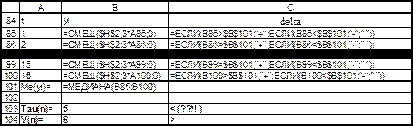
Рис. 18. Определение наличия тренда с помощью критерия серий, основанном на медиане выборки (режим отображения формул)

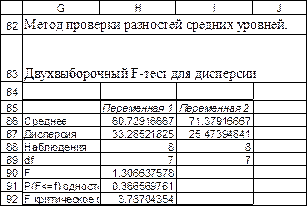
Рис. 19. Определение наличия тренда с помощью метода проверки разностей средних уровней. Проверка равенства дисперсий для двух отрезков временного ряда.

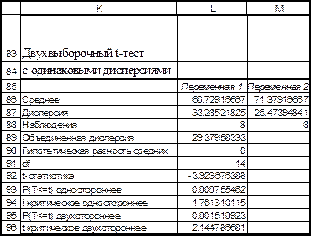
Рис. 20. Определение наличия тренда с помощью метода проверки разностей средних уровней. Проверка равенства средних для двух отрезков временного ряда.

Для исследования автокорреляционной функции временного ряда (АКФ) вычислим последовательность коэффициентов автокорреляции уровней первого, второго и т.д. до пятого порядка включительно. Расчеты приведены на рис.21-22.

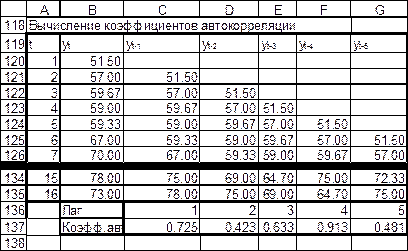
Рис.21. Вычисление коэффициентов автокорреляции, режим отображения данных

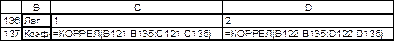
Рис. 22. Вычисление коэффициентов автокорреляции, режим отображения формул

График АКФ (коррелограмма) показана на рис.23. Поскольку при лаге, равном четырем, АКФ принимает наиболее высокое значение, равное 0.915, можно утверждать, что ряд имеет сезонную составляющую с периодом равным 4.

Можно отметить, что значение АКФ при лаге, равном единице, тоже велико (0.725) - это также служит подтверждением наличия тренда, который целесообразно аппроксимировать линейной функцией.

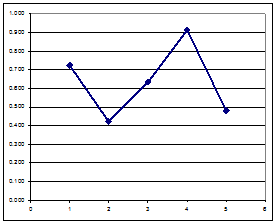
Рис. 23. Коррелограмма временного ряда

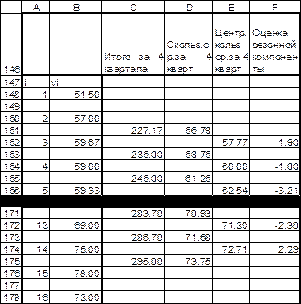
Рис.24. Выравнивание исходного ряда методом скользящей средней, режим отображения данных.

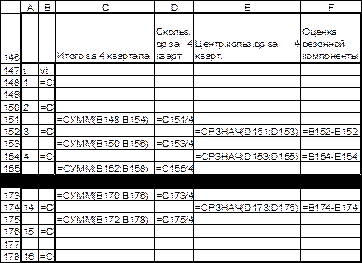
Рис. 25. Выравнивание исходного ряда методом скользящей средней, режим отображения формул.

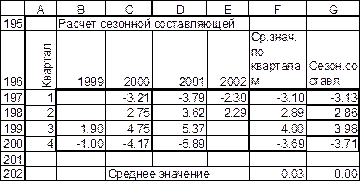
Рис. 26. Расчет значений сезонной компоненты, режим отображения данных.

Дальнейшие расчеты приведены на рис.28-30. Выровненные данные 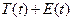приведены в диапазоне D204: D220, они получены вычитанием сезонной компоненты из исходных уровней ряда.

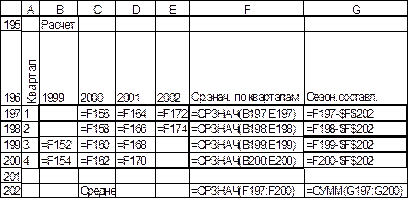
Рис. 27. Расчет значений сезонной компоненты, режим отображения формул

Аналитическое выравнивание уровней 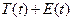проведено с помощью функции ЛИНЕЙН(), результат содержится в диапазоне B223: C227.

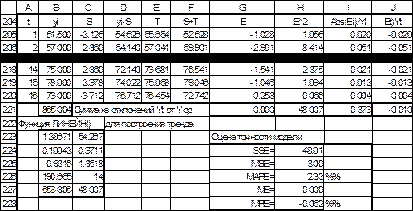
Рис. 28. Расчет значений трендовой и случайных компонент и оценка точности модели, режим отображения данных

В результате получена зависимость 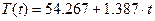, которая описывает линейный тренд. Расчетные значения 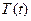приведены в диапазоне Е204: Е220, они получены с помощью найденной зависимости.

Расчетные значения, полученные по формуле 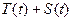, показаны в диапазоне F204: F220.

Расчетные значения случайной компоненты , полученные по модели, показаны в диапазоне Е204: Е220.

Проведем оценку точности полученной модели.

Расчеты приведены на рис.29-30. Сумма квадратов отклонений (SSE) равна 48.01, содержится в ячейке H221 и Н224. Средний квадрат ошибки (MSE) равен 3.00 и содержится в ячейке H225. Средняя абсолютная процентная ошибка (MAPE) равна 2.33 %, поскольку это значение меньше 10%, то модель характеризуется высокой точностью.

Для оценки несмещённости оценки прогноза вычислим среднюю ошибку МЕ и среднюю процентную ошибку МРЕ. Средняя ошибка МЕ равна нулю с точностью до трех знаков, средняя процентная ошибка МРЕ равна -0, 06%, что меньше 5%. Это свидетельствует о несмещенности прогноза.

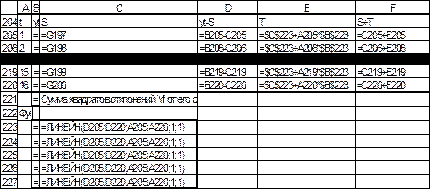
Рис. 29. Расчет значений трендовой и случайной компонент и оценка точности модели, режим отображения формул (начало)

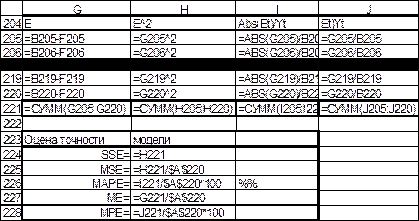
Рис. 30. Расчет значений трендовой и случайной компонент и оценка точности модели, режим отображения формул (окончание)