Оценка качества построенной модели

Для этого исследуем ряд остатков 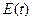, т.е. отклонения расчетных значений от фактических данных. Их значения показаны на рис.31, диапазон А230: В246.

Для проверки случайности остатков используем критерий поворотных точек. Для этого строим график остатков (рис.32) и подсчитываем количество поворотных точек. Количество поворотных точек р равно 9. Критическое значение р равно 6. Поскольку неравенство (25) соблюдается, то нет оснований отвергнуть гипотезу о случайности ряда остатков с уровнем значимости 5% процентов.

Проверка равенства математического ожидания уровней ряда остатков нулю осуществляется с помощью критерия Стьюдента используя соотношение (22). С этой целью в ячейках Н247 и Н248 на рис.34-35 вычисляются значения и 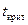соответственно. Значения используемых в формуле величин содержатся в диапазоне G230: H245, они получены с помощью надстройки «Пакет анализа» MS Excel. Поскольку , гипотеза о равенстве нулю математического ожидания уровней ряда остатков подтверждается

Рис. 31. Значения случайной компоненты (остатки)

.

Проверку соответствия ряда остатков нормальному закону распределения проведем с помощью RS- критерия. Расчетное значение RS находится в ячейке Н250, и оно равно 3.24. Это значение попадает между табулированными границами (табл.3) с заданным уровнем значимости, поэтому гипотеза о нормальном распределении ряда остатков принимается

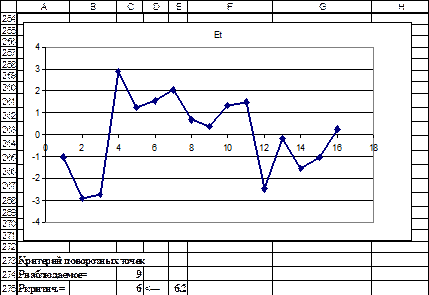
Рис. 32. График остатков и проверка их случайности.

Рис.33. Проверка случайности остатков, режим отображения формул.

Проверку наличия автокорреляции в остатках проведем с помощью критерия Дарбина – Уотсона [5]. Вычисление по формуле (38):

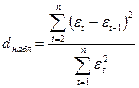
(38)

Значение приведено на рис.31 в ячейке С249 и оно оказалось равным 1.384. По таблицам (зная количество наблюдений n =16; количество параметров один –время и уровень значимости 5%) находим два критических значения (табличных уровня): нижний - 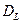=1.1 и верхний - 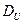=1.37. Поскольку - остатки некоррелированы, это условие адекватности модели выполнено.

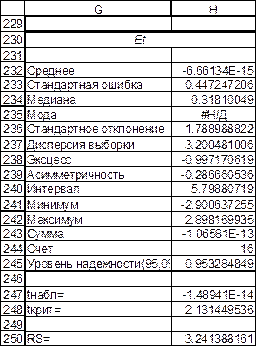
Рис. 34. Описательная статистика остатков и проверка равенства нулю среднего и их нормальности.

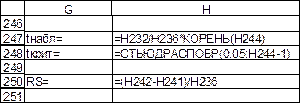
Рис. 35. Описательная статистика остатков и проверка равенства нулю среднего и их нормальности, режим отображения формул

Построение точечных и интервальных прогнозов. Все вычисления приведены на рис. 36-37.

Для вычисления точечного прогноза в построенную модель подставляем соответствующие значения фактора в формулу (36). Искомые значения содержатся в интервале В283: В286.

Полуширина доверительного интервала для линейной модели рассчитывается по формуле (37) и содержится в интервале Е283: Е286. Верхняя и нижняя границы прогноза равны 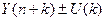; содержатся в интервале G283: H286. График прогнозных значений приведен на рис.39. Граница прогноза равна .

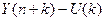Рис. 36.Вычисление прогнозных значений, режим отображения данных

Рис. 37. Вычисление прогнозных значений, режим отображения формул (начало).

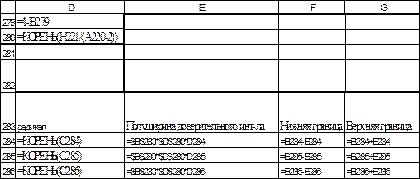
Рис. 38. Вычисление прогнозных значений, режим отображения формул (окончание).

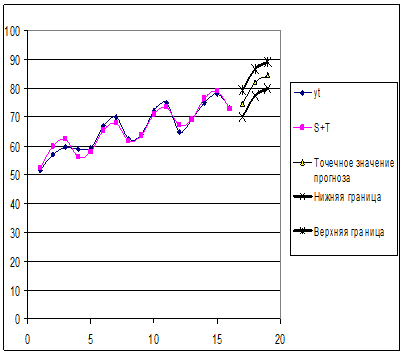
Рис. 39. График прогнозных значений.

Выводы:

1) Модель имеет вид:

;

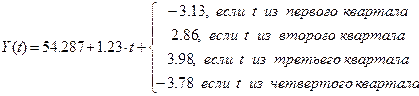2) Модель является адекватной по всем критериям.

3) Модель несмещённая и обладает высокой степенью точности.

4) Прогнозные объемы продаж в первых трех кварталах 2003 года составят с вероятностью 95% 74.715±4.530, 82.088± 4.638 84.593±4.755 соответственно.

Задание

Каждый вариант содержит одну задачу. Исходные данные, описывающие динамику экономической системы за некоторый промежуток времени, выдаются преподавателем. Необходимо провести анализ структуры временного ряда, построить модель и провести прогноз на три момента времени вперед.

Исполнение: Выполнение индивидуального задания с использованием MS Excel или любого статистического пакета. Интерпретация результатов решения.

Список литературы

1. Арженовский С.В. Статистические методы прогнозирования. Учебное пособие / Арженовский С.В., Молчанов И.Н. – Ростов н/Д: РИО Рост.гос.экон.универ. 2001 – 74 с.

2. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА, 2001 – 402 с.

3. Магнус Я.Р. Эконометрика. Начальный курс / Магнус Я.Р., Катышев П.К., Пересецкий А.А. – М.: Дело, 2006 – 400 с.

4. Практикум по эконометрике/ Под ред. И.И. Елисеевой. – М.: Финансы статистика, 2001, 192 с.

5. ЭКОНОМЕТРИКА. Множественная регрессия. Методические указания к лабораторным работам / Беляев В.В., Виноградова Т.А., Косовцева Т.Р .- СПб: СПГГИ(ТУ), СПб, 2009., 61 с

6. ЭКОНОМЕТРИКА. Парная регрессия. Методические указания к лабораторным работам / Беляев В.В., Виноградова Т.А., Косовцева Т.Р .- СПб: СПГГИ(ТУ), СПб, 2009., 55 с.

7. ЭКОНОМЕТРИКА: Учебник/ Елисеева И.И. Курышева С.В., Гордеенко Н.М. Костеева Т.В. и др. – М.: Финансы и статистика, 2005. -576 с.: ил.

8. ЭКОНОМЕТРИКА. Ч1. Элементы теории вероятностей и математической статистики. Методические указания для выполнения лабораторных работ / Беляев В.В., Виноградова Т.А., Косовцева Т.Р. - СПб: СПГГИ(ТУ), 2008., 72 с.

9. ЭКОНОМЕТРИКА. Ч2. Элементы теории вероятностей и математической статистики: Методические указания для выполнения лабораторных работ / Беляев В.В., Виноградова Т.А., Косовцева Т.Р .- СПб: СПГГИ(ТУ),, 2008. 64 с

10. Материалы сайта https://zoonek2.free.fr/UNIX/48_R/15.html

Приложение 1

Таблица П1.