
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Коэффициенты ассоциации и контингенции предназначены для количественной характеристики многомерных связей социально – экономических явлений
|
|
Коэффициенты ассоциации и контингенции предназначены для количественной характеристики многомерных связей социально – экономических явлений. Они характеризуют тесноту взаимосвязи двух качественных признаков, каждый из которых состоит только из двух значений. При исследовании связи числовой материал располагают в виде таблиц сопряженности 2 х 2 (табл.55).
Для вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака.
Таблица 55
Схема группировки для расчета коэффициентов
| а | b | a+b |
| c | d | c+d |
| a+c | b +d | a+b+c+d |
Коэффициент ассоциации определяется:
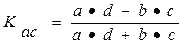
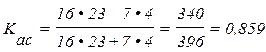
Коэффициент ассоциации говорит о тесной связи между рождаемостью и степенью обеспеченности жильем.
Коэффициент определяется по формуле:
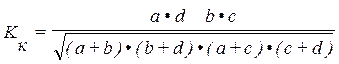
Таким образом, вычислим связь между двумя качественными признаками рождаемостью и степенью обеспеченности жильем:

Таким образом, можно сделать вывод, что связь между рождаемостью и степенью обеспеченности жильем заметная, т. к. Кк ≥ 0, 3.[7] Однако коэффициент контингенции дает более осторожную оценку степени тесноты связи, чем коэффициент ассоциации.
Пример 2. Имеются следующие данные о прибыли от реализации услуг и выручке от реализации услуг 40 гостиничных хозяйств гостиниц, приведенные в таблице 56.
Таблица 56
Прибыль и валовая выручка по совокупности гостиниц
| Валовая выручка, млн. руб., х | Прибыль от реализации услуг, млн. руб., у | Число гостиниц |
| 300-400 | 10-20 | |
| 400-500 | 10-20; 20-30 | 4; 1 |
| 500-600 | 10-20; 20-30; 30-40 | 2; 5; 4 |
| 600-700 | 20-30; 30-40; 4 0-50 | 3; 8; 2 |
| 700-800 | 30-40; 4 0-50; 50-60 | 2; 4; 3 |
Установить взаимосвязь прибыли от реализации услуг с выручкой от реализации услуг гостиничных хозяйств по данным интервальной группировки.
Решение.
1. По средним данным интервальной группировки заполняется корреляционная таблица (табл. 57).
Средние значения 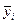 (прибыли от реализации услуг) и
(прибыли от реализации услуг) и 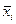 (валовая выручка) определяются по формуле средний арифметической взвешенной:
(валовая выручка) определяются по формуле средний арифметической взвешенной:
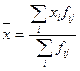 и
и 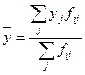
Таблица 57
Корреляционная таблица
| Валовая выручка, млн. руб., х | Прибыль от реализации услуг, млн. руб., у | Итого |
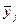
| ||||
| - | - | - | - | 15, 0 | |||
| - | - | - | 17, 0 | ||||
| - | - | 26, 82 | |||||
| - | - | 34, 23 | |||||
| - | - | 46, 11 | |||||
| Итого | 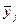 =31, 75 =31, 75
| ||||||
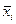
| 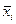 =605 =605
| - |
Относительно этих средних значений ведется весь дальнейший расчёт. Так, например, для второй группы гостиниц, расчет будет выглядеть следующим образом:
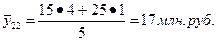 ;
;
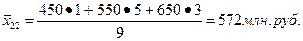 ;
;
Корреляционная таблица свидетельствует о наличии прямой связи между валовой выручкой и прибылью от реализации услуг, т. к. их количества расположились вокруг диагонали идущей от верхнего левого угла к нижнему правому. Также в таблице указаны средние значения валовой выручки и прибыли от реализации по гостиницам.
Для оценки тесноты связи рассчитывается вспомогательная таблица 58.
Таблица 58
Расчетные данные
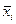
| 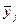
| 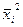
| 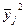
| 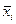 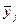
| 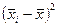
| 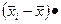
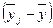
|
| 26, 82 | -151 | |||||
| 34, 23 | ||||||
| 46, 11 | ||||||
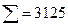
| 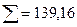
| 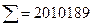
| 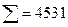
| 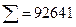
| 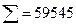
| 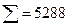
|

рассчитываем линейный коэффициент корреляции:
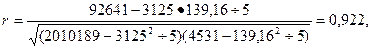
что указывает на очень сильную прямую зависимость между валовой выручкой и прибылью от реализации услуг.
Для проверки значимости этого коэффициента определяется расчётное значение критерия Стьюдента по формуле:
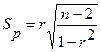 ,
,
соответственно 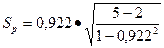 .
.
Табличное значение критерия Стьюдента при расчетном числе степеней свободы 3 равняется 0, 137-3, 182 с вероятностью 0, 9-0, 05. Фактическое значение критерия больше расчётного значения, поэтому найденный коэффициент корреляции следует считать значимым.
Далее по формулам:
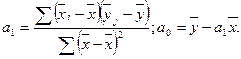
Определим параметры линейного уравнения регрессии:
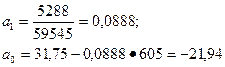
Таким образом, изучаемая взаимосвязь может быть выражена уравнением прямой линии в виде yх = -21, 94+0, 089x.
Отрицательность коэффициента 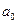 интерпретации не подлежит. Приняв y=0, получим x=21, 94/0, 089=244, 4 млн. руб. – что и будет «точкой безубыточности» гостиниц.
интерпретации не подлежит. Приняв y=0, получим x=21, 94/0, 089=244, 4 млн. руб. – что и будет «точкой безубыточности» гостиниц.
Определим универсальный индекс корреляционной связи, для чего в приведенной ниже таблице 59 даны расчеты числителей формул фактической и аналитической дисперсии.
Таблица 59
Расчетные данные для индекса корреляции
| Для фактической дисперсии | Для аналитической дисперсии | ||
| 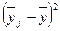
| 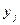 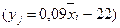
| 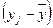
|
| 18, 5 | 175, 6 | ||
| 29, 5 | 5, 1 | ||
| 26, 82 | 24, 6 | 35, 2 | 11, 9 |
| 34, 23 | 6, 2 | 42, 5 | 115, 6 |
| 46, 11 | 206, 2 | 45, 5 | |
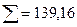
| 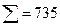
| 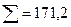
| 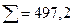
|
По суммам из этой таблицы определим дисперсии отклонений в размерности млн. руб.2 : 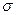 2 уф = 735/5=147;
2 уф = 735/5=147; 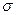 2 уа =49765=99;
2 уа =49765=99; 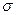 2 уо = 147-99, 4=47, 6. Таким образом по формуле индекса корреляционной связи:
2 уо = 147-99, 4=47, 6. Таким образом по формуле индекса корреляционной связи:
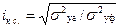 ,
,
Определяем, что индекс корреляционной связи равняется 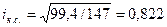 , что также свидетельствует о достаточной тесной связи между валовой выручкой и прибылью от оказанных услуг.
, что также свидетельствует о достаточной тесной связи между валовой выручкой и прибылью от оказанных услуг.
Дисперсии отклонений позволяют оценить и значимость параметров уравнения по критерию Стьюдента, а также всего уравнения на адекватность – по критерию Фишера. Так, по формуле:
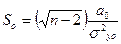
Рассчитанное значение критерия Стьюдента для параметра 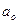 равняется:
равняется:
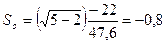
а для параметра  соответственно по формуле:
соответственно по формуле:
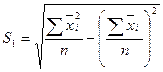 ,
,
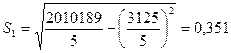
Рассчитанные критерии Стьюдента оказались меньше табличного, значит, параметры сформированного уравнения регрессии не являются значимыми.
Расчётное значение критерия Фишера по формуле:
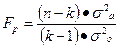
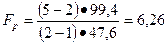
а его табличное значение при степенях свободы 3 и 1 даже при значимости 0, 05 составит 10, 13. Оно больше расчётного, значит, построенное уравнение прямой линии отражает фактическую взаимосвязь неадекватно.
Рассмотренный пример показал возможность противоречивых выводов в результате корреляционного и регрессионного анализа.
Для корреляционно – регрессионного анализа необходимо брать факторы, не взаимосвязанные между собой. В данном случае прибыль от оказанных услуг гостиниц является составляющей валовой выручки, т.е. прибыль и выручка взаимосвязаны между собой.
Пример 3. Имеются следующие данные по группе гостиничных предприятий за отчетный год (табл. 60).
Таблица 60
Данные о производительности труда, фондовооруженности, текучести кадров и интегральном показателе использования рабочего времени по совокупности гостиниц
| № предприятия | Годовая производительность труда, чел./тыс. руб. | Фондо- вооруженность тыс.руб./чел. | Удельный вес оборудования в основном капитале | Текучесть кадров, % | Интегральный показатель использования Рабочего времени |
| 15, 2 | 0, 39 | 9, 1 | 0, 96 | ||
| 12, 8 | 0, 29 | 10, 1 | 0, 80 | ||
| 13, 8 | 0, 34 | 5, 0 | 0, 84 | ||
| 14, 0 | 0, 36 | 7, 0 | 0, 86 | ||
| 16, 3 | 0, 47 | 9, 0 | 0, 98 | ||
| 12, 6 | 0, 28 | 4, 0 | 0, 83 | ||
| 13, 2 | 0, 32 | 12, 0 | 0, 87 | ||
| 12, 9 | 0, 29 | 6, 5 | 0, 84 | ||
| 13, 1 | 0, 33 | 8, 0 | 0, 81 | ||
| 12, 5 | 0, 28 | 7, 00 | 0, 85 | ||
| 15, 7 | 0, 40 | 8, 5 | 0, 97 | ||
| 13, 5 | 0, 34 | 5, 0 | 0, 83 |
На основании приведенных данных:
1) составьте уравнение множественной зависимости производительности труда, обосновав систему факторов, включённых в модель;
2) определите совокупный коэффициент корреляции и частные коэффициенты корреляции;
3) сопоставьте роль различных факторов в формировании моделируемого показателя.
По результатам расчетов сделайте выводы.
Решение.
Результативный показатель y – годовая производительность труда.
Признаки - факторы:
Фондовооруженность - 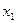 ;
;
Удельный вес оборудования в основном капитале - 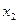 ;
;
Текучесть кадров - 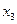 ;
;
Интегральный показатель использования рабочего времени -  .
.
Для определения возможности включения факторов в модель строится матрица парных коэффициентов корреляции в таблице 61 (с использованием ЭВМ или рассчитывается по формуле линейного коэффициента корреляции, см. пример 1).
Таблица 61
Матрица парных коэффициентов корреляции
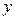
| 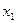
| 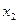
| 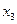
| 
| |
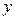
| |||||
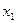
| 0, 911 | ||||
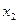
| 0, 903 | 0, 977 | |||
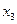
| 0, 249 | 0, 264 | -0, 009 | ||

| 0, 979 | 0, 812 | 0, 710 | 0, 710 |
Значения матрицы парных коэффициентов корреляции показывают, что фактор 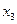 не следует включать в модель, так как связь результативного показателя с ним слабая (
не следует включать в модель, так как связь результативного показателя с ним слабая (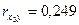 ). С остальными факторами связь тесная, и, если нет мультиколлинеарности, они могут быть включены в модель.
). С остальными факторами связь тесная, и, если нет мультиколлинеарности, они могут быть включены в модель.
Сначала проверяется возможность включения в модель факторов 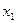 и
и 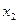 . В качестве критериев принимается соблюдение следующих неравенств:
. В качестве критериев принимается соблюдение следующих неравенств:

Фактически эти неравенства не соблюдаются, так как
0, 911< 0, 977;
0, 903< 0, 977.
Следовательно, в модель должен быть включен фактор 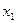 , так как связь результативного показателя с факторным наиболее тесна (
, так как связь результативного показателя с факторным наиболее тесна (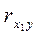 =0, 911).
=0, 911).
Далее проверяется возможность включения в модель факторов 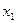 и
и  , аналогично предыдущему пункту, в результате мы получаем:
, аналогично предыдущему пункту, в результате мы получаем:
0, 911> 0, 812;
0, 979> 0, 812.
Таким образом, в модель множественной зависимости могут быть включены два фактора: 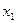 и
и  , тогда линейное уравнение имеет следующий вид:
, тогда линейное уравнение имеет следующий вид:
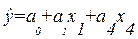 .
.
Система нормальных уравнений для нахождения параметров 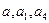 следующая:
следующая:
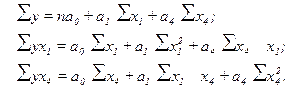
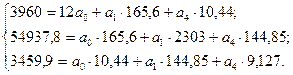
Решение системы уравнений даёт следующие значения параметров:
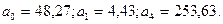
Модель зависимости производительности труда от факторов имеет следующий вид:
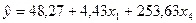
Значения результативного признака, рассчитанные по уравнению связи, представлены в таблице 62.
Таблица 62
Вспомогательная таблица для расчёта ошибки модели
| № предприятия | Годовая производительность труда, чел./тыс. руб.
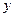
| Теоретический уровень годовой производительность труда, тыс. руб. /чел. 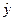
| 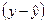
| 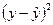
|
| 359, 1 | +0, 9 | 0, 81 | ||
| 307, 8 | -9, 8 | 96, 04 | ||
| 332, 4 | -4, 4 | 19, 36 | ||
| 328, 4 | +1, 6 | 2, 56 | ||
| 369, 0 | -3, 0 | 9, 00 | ||
| 314, 6 | +1, 4 | 1, 96 | ||
| 324, 4 | +9, 6 | 92, 16 | ||
| 318, 9 | -18, 5 | 342, 25 | ||
| 311, 7 | +2, 3 | 5, 29 | ||
| 319, 2 | +0, 8 | 0, 64 | ||
| 363, 8 | -1, 8 | 3, 24 | ||
| 328, 3 | +3, 7 | 13, 69 | ||
| итого | 587, 00 |
По данным этой же таблицы исчисляется средняя квадратическая ошибка уравнения:
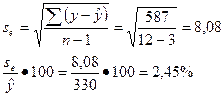
Следовательно, уравнение хорошо отображает взаимосвязь производительности труда и двух её факторов.
Определяется множественный коэффициент корреляции по следующей формуле:
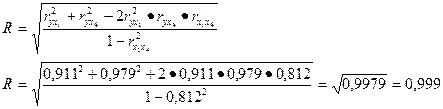
Парные коэффициенты корреляции взяты из таблицы 61.
Близость коэффициента множественной корреляции к единице означает: роль не учтенных в модели факторов ничтожна, и есть основания считать, что параметры регрессионной модели отражают степень эффективности включённых а неё факторов.
Частные коэффициенты корреляции следующие:
a) Частный коэффициент корреляции между результативным признаком 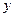 и фактором
и фактором 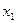 при элиминировании фактора
при элиминировании фактора  :
:
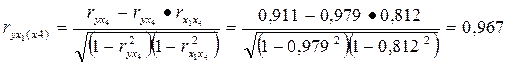
б) Частный коэффициент корреляции между результативным признаком 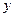 и фактором
и фактором  при элиминировании фактора
при элиминировании фактора 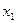 :
:
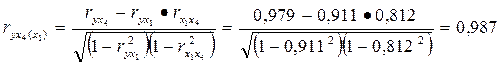
Сопоставление полученных частных коэффициентов корреляции с вычисленными ранее парными коэффициентами корреляции подтверждают наличие тесной связи между результативным и факторным признаком.
Для сравнения доли отдельных факторов в формировании показателя производительности труда определим коэффициенты эластичности:
1). Для фактора х1
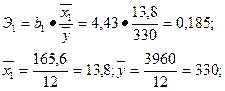
2). Для фактора х4:
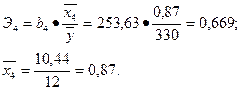
Следовательно, при увеличении фондовооруженности труда на 1% производительность труда возрастает лишь на 0, 185%. Увеличение показателя использования рабочего времени на 1% повлечет рост производительности труда на 0, 669%.
Пример 4. По группе туристических агентств имеются данные (табл.63).
Таблица 63
Время выхода рекламы и объем оказанных туристических услуг в агентствах
| № предприятия | время выхода рекламы, мин. | Объем реализации турпакетов, тыс. руб. |
Оцените степень тесноты связи между показателями время выхода рекламы и объемом реализации турпакетов при помощи коэффициента Фехнера.
Решение.
Для расчёта коэффициента Фехнера составляется вспомогательная таблица 64.
Таблица 64
Расчетные данные
| время выхода рекламы, мин. | 
| Объем реализации турпакетов, тыс. руб. | 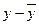
|
| -22 | -16 | ||
| -47 | |||
| -8 | -21 | ||
| -23 | -81 | ||
| -4 | -1 | ||
| -5 | |||
| -5 | |||
| -13 | -13 | ||
| -8 | -27 | ||
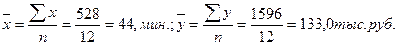
Коэффициент Фехнера определяется по формуле:
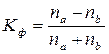 , где
, где
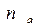 - число совпадений отклонений признака а и признака в от их средних величин по знаку
- число совпадений отклонений признака а и признака в от их средних величин по знаку
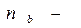 число несовпадений
число несовпадений
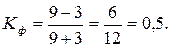
Полученное значение коэффициента свидетельствует о наличии связи между временем, которое потрачено фирмами на рекламу и объёмом реализации услуг.
Задание 1. Имеются следующие данные по ранжированному ряду регионов ЦФО РФ по коэффициенту рождаемости (табл. 11).
Определите с помощью коэффициента Фехнера взаимосвязь между показателем рождаемости и стоимостью валового регионального продукта на душу населения. Сделайте выводы
Задание 2. Имеются следующие данные о стаже работников и среднемесячной заработной платой (табл. 65).
Таблица 65
Группировка работников по стажу и среднемесячной заработной плате
| Группы сотрудников по стажу | Число сотрудников в группе | Среднемесячная заработная плата, руб. | Дисперсия месячной заработной платы в группе |
| До 3 лет | |||
| 3 года и более |
Определите непараметрические критерии и вычислите степень тесноты взаимосвязи между стажем работы и размером заработной платы работников.
Задание 3. Имеются следующие данные о посещении спортивных клубов (табл. 66)
Таблица 66
Группировка населения по посещаемости спортивных клубов и наличию семьи, тыс. чел.
| Посещения спортивных клубов, X | Семейное положение, Y | |
| семейные | холостые | |
| Посещают | 2, 5 | 4, 5 |
| Не посещают | 10, 0 | 14, 5 |
Оцените взаимосвязь посещения спортивных клубов и семейного положения, исчислив коэффициенты ассоциации и контингенции.
Задание 4. По группе гостиничных хозяйств имеются данные (табл. 67).
Таблица 67
Данные о средней стоимости номера и выручке выборочной совокупности гостиниц
| № предприятия | Средняя стоимость номера, $ | Выручка, тыс. $ |
Необходимо оценить степень тесноты связи между показателями средней стоимости номера и выручкой при помощи коэффициента Фехнера.
Задание 5. Имеются следующие данные о работе гостиниц (табл. 68).
Таблица 68
Данные о выручке, стоимости номера, текучести кадров и средствах на рекламную деятельность совокупности гостиниц
| № предприятия | Выручка, тыс. $ | Средняя стоимость номера, $ | Текучесть кадров, % | Денежные средства, потраченные на рекламу, тыс. $ |
| 3, 1 | 1, 5 | |||
| 4, 1 | 2, 5 | |||
| 4, 0 | 0, 6 | |||
| 2, 8 | ||||
| 3, 0 | 0, 8 | |||
| 2, 5 | 1, 5 | |||
| 3, 2 | 1, 8 | |||
| 4, 5 | 0, 8 | |||
| 3, 8 | 0, 9 | |||
| 3, 0 | 1, 2 |
На основании приведенных данных:
1) составьте уравнение множественной регрессии, используя выручку в качестве результативного фактора и обосновав систему факторов, включённых в модель;
2) определите совокупный коэффициент корреляции и частные коэффициенты корреляции;
3) дайте критериальную оценку полученным показателям;
4) сопоставьте роль различных факторов в формировании моделируемого показателя.
Сделайте выводы по результатам расчетов.
Задание 6. Имеется следующие данные о группировке населения РФ (табл. 69).
Таблица 69
Группировка населения РФ по состоянию в браке и возрастным группам населения по данным переписи 2002 г., тыс. чел.
| Показатель | Численность населения по возрасту, тыс. чел. | всего | |
| До 25 лет | Старше 25 лет | ||
| Состоят в браке | 31, 21 | 31, 18 | 62, 39 |
| Не состоят в браке | 20, 49 | 22, 77 | 43, 26 |
| Всего | 51, 70 | 53, 95 | 105, 65 |
С помощью непараметрических критериев определите степень взаимосвязи между возрастом и состоянием в браке исчислив показатели ассоциации, контингенции.
Контрольные вопросы
1. Понятие о связях между явлениями.
2. Виды и формы корреляционной зависимости.
3. Методы исследования связей.
4. Однофакторный и много факторный корреляционно -регрессионный анализ.
5. Проверка построенной модели на адекватность.
6. Показатели тесноты связи.
7. Непараметрическая оценка связей. Коэффициенты ассоциации, контингенции, коэффициент Фехнера.