Решение. Найдем частоту свободных колебаний по формуле

Найдем частоту свободных колебаний по формуле 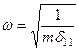. Перемещение 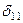ищем методом Максвелла – Мора

.

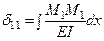Для построения эпюры изгибающих моментов 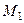приложим в точке, где расположена сосредоточенная масса, единичную силу по направлению возможного перемещения массы. В данном примере сосредоточенная масса может перемещаться только по вертикали и эпюра моментов от единичной силы показана на рис. 3, а. Интегрирование формулы Максвелла – Мора по правилу Верещагина дает:

.

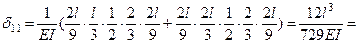
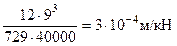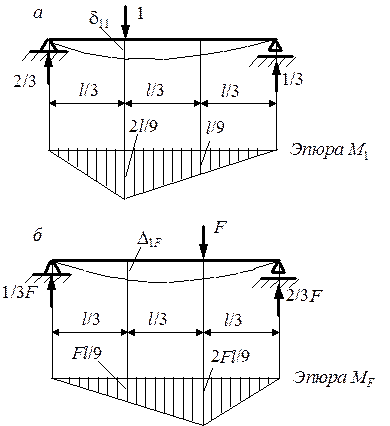
Рис.3

Обратите внимание на единицы измерения величины 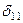. Подставим 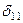в формулу 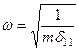. Вспомним, что 1 кН = 10³ Н = 10³ кг м /сек², после подстановки массы 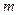в " кг " получим круговую частоту свободных колебаний в " сек^–1":

.

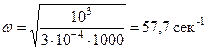Теперь определим амплитудное значение силы инерции, используя формулу 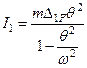. Чтобы воспользоваться этой формулой найдем величину 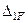– перемещения по направлению движения массы от амплитудного значения силы 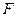. В соответствии с методом Максвелла – Мора это перемещение

.

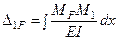Эпюра 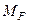от действия амплитудного значения 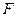показана на рис. 3, б. Перемножая эпюры 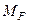и 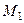по правилу Верещагина найдем

.

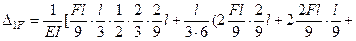
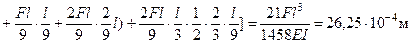Частота вынужденных колебаний согласно условию

.

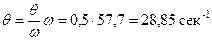Тогда амплитудное значение силы инерции по формуле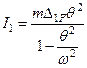

.

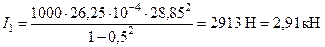Окончательная эпюра изгибающих моментов от динамического действия нагрузки, построенная с учетом формулы 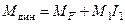, показана на рис. 4.

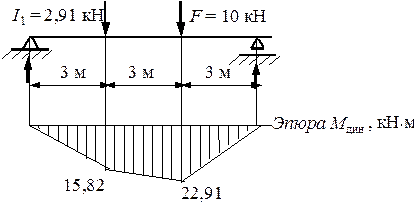
Рис.4