Решение. В случае плоских колебаний рассматриваемая упругая система имеет две степени свободы

В случае плоских колебаний рассматриваемая упругая система имеет две степени свободы. Единичные перемещения 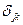определяется по правилу Верещагина, перемножая соответствующие эпюры единичных изгибающих моментов (рис.2, б)

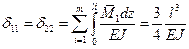
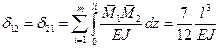
Используя формулу 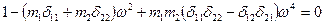, находим собственные частоты

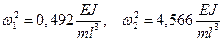
Определяем далее собственные формы колебаний, подставляя 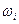и 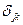в выражение

.

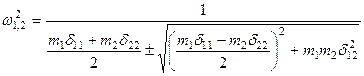В результате для собственной формы

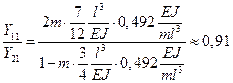
или 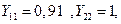а для второй .

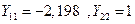Используя 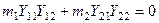, убедимся, что полученные собственные формы обладают свойством ортогональности:

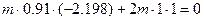
Для определения амплитуд колебаний воспользуемся решением системы

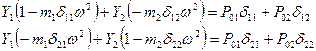(1)

при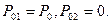

Тогда

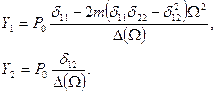(2)

Здесь 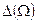- определитель системы (1), описываемый выражением

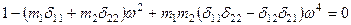, если в последнем принять 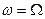. Нетрудно видеть, что при

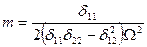(3)

числитель в выражении для 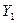обращается в нуль. На этом основан принцип динамического гасителя колебаний. При заданной частоте 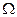амплитуды перемещений и сил, действующих на массы определяются следующими выражениями:

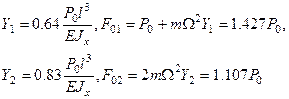
Эпюра динамических моментов представлена на рис.2.

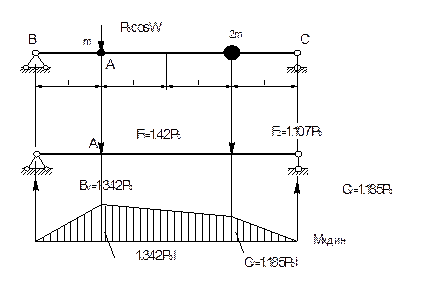
Рис.2