Пример 31.

Определить низшую частоту собственных колебаний балки методом Релея, если вес единицы ее длины равен 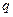(рис. 1).

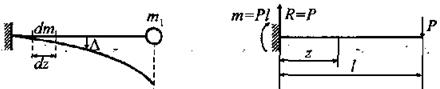
а) б)

Рис. 1

Решение.

Найдем сначала приближенное выражение изогнутой оси балки. Для этого к концу балки приложим поперечную силу Р. Согласно методу начальных параметров, прогиб произвольной точки с координатой z будет:

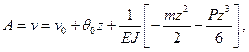
или, так как 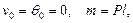то

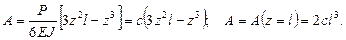(1)

Вычислим потенциальную энергию согласно :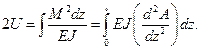

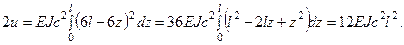(2)

Знаменатель в формуле Релея 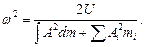с учётом (1) будет равен:

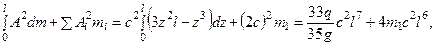(3)

поэтому, согласно (2), (3) и формулы Релея имеем:

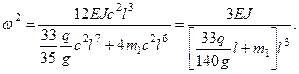
Точное решение этой же задачи есть:

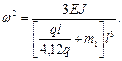
При 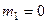легко подсчитать ошибку приближённого решения. Она составляет всего 1, 5%.

Пример 32.

Определить методом Релея низшую частоту собственных колебаний системы, состоящей из стержня и присоединенной к ней массы m. Масса стержня равна M (рис. 1).

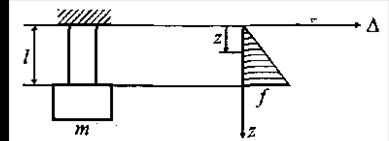
Рис. 1

Решение.

Примем для перемещения поперечного сечения стержня выражение:

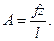(1)

Согласно 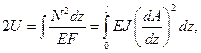с учётом (1), получим:

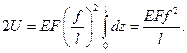(2)

Знаменатель в формуле Релея :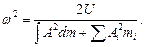

(3)

Подставляя (2) и (3) в формулу Релея, найдём:

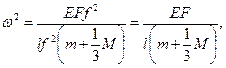
где 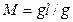- масса стержня. Величина 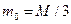носит название приведенной массы. Коэффициент 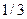- коэффициент приведения массы. Он показывает, какую часть массы стержня нужно присоединить к сосредоточенной массе m чтобы свести упругую систему к системе с одной степенью свободы. Если масса стержня 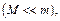то