
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. 1. Определение статического прогиба в сечении С балки КD и статического напряжения в сечении у заделки А
|
|
1. Определение статического прогиба в сечении С балки КD и статического напряжения в сечении у заделки А. Из уравнений равновесия статики 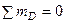 и
и 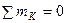 найдем опорные реакции в балке КD (рис. 8.4, б):
найдем опорные реакции в балке КD (рис. 8.4, б):
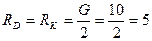 кН.
кН.
На балку АВ в точке В (К) опоры на консоль передается нагрузка Р = 5 кН, равная по величине опорной реакции RK , но обратная по направлению. Из уравнений 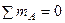 и
и 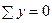 определяем реактивные усилия в заделке А балки АВ: МA = 10 кНм; RА = 5 кН. Определив опорные реакции в балках, строим эпюры поперечных сил Q и изгибающих моментов М для балок КD и АВ (рис. 1, в, г, е, ж). Зная величины изгибающих моментов, возникающих в опасных сечениях балок, определяем статические напряжения в сечениях С и А:
определяем реактивные усилия в заделке А балки АВ: МA = 10 кНм; RА = 5 кН. Определив опорные реакции в балках, строим эпюры поперечных сил Q и изгибающих моментов М для балок КD и АВ (рис. 1, в, г, е, ж). Зная величины изгибающих моментов, возникающих в опасных сечениях балок, определяем статические напряжения в сечениях С и А:
 кН/м2;
кН/м2;
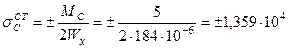 кН/м2.
кН/м2.
Для определения статического прогиба в точке С балки КD вначале предполагаем, что эта балка опирается на абсолютно жесткое основание. Используя метод начальных параметров, составляем уравнение прогибов, приняв начало координат в сечении D.
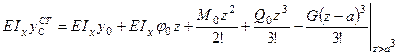 ,
,
где y 0 = 0, М 0 = 0, 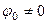 ,
, 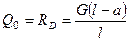 .
.
Для нахождения 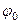 составим уравнение прогиба для сечения К в котором прогиб равен нулю из условий закрепления:
составим уравнение прогиба для сечения К в котором прогиб равен нулю из условий закрепления:
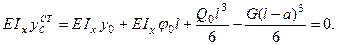
Так как 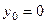 , то, решая это уравнение, получим:
, то, решая это уравнение, получим:
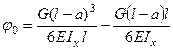 .
.
Подставив найденное значение 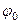 в уравнение прогиба для сечения С, получим формулу для определения
в уравнение прогиба для сечения С, получим формулу для определения 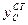 :
:
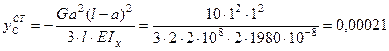 м.
м.
Для вычисления полного перемещения сечения С с учетом характера опирания балки КD на консольную балку необходимо найти прогиб консольной балки АВ от действия на нее силы РK = - RK = 5 кН. Для этого, приняв начало координат в сечении В балки АВ, составим уравнение метода начальных параметров для определения прогиба на конце консоли. При начале координат в точке В консоли известными параметрами будут: М 0 = МB = 0; Q 0 = QB = - РK = -5 кН, а неизвестными 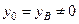 ;
; 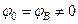 . Неизвестные начальные параметры y 0 и
. Неизвестные начальные параметры y 0 и 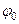 определим из уравнений прогиба и угла поворота для сечения А. Из условия закрепления балки АВ имеем при z = l = 2 м:
определим из уравнений прогиба и угла поворота для сечения А. Из условия закрепления балки АВ имеем при z = l = 2 м: 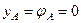 .
.
Составим уравнения метода начальных параметров:
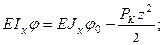 (1)
(1)
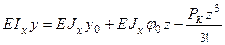 . (2)
. (2)
Приравняв к нулю уравнение (1) при z = l м, определяем 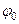 :
:
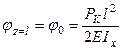 .
.
Подставив найденное значение 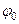 в уравнение (2) и принимая y = 0 при z = l, получим выражение второго неизвестного начального параметра y 0 , определяющего прогиб сечения В консольной балки АВ:
в уравнение (2) и принимая y = 0 при z = l, получим выражение второго неизвестного начального параметра y 0 , определяющего прогиб сечения В консольной балки АВ:
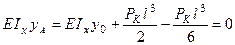 ;
;
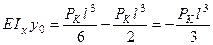 ;
;
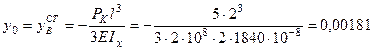 м.
м.
Знак “минус” говорит о том, что конец консольной балки переместится вниз.
Определив прогиб 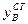 и изобразив эпюру перемещений системы (рис. 1, з), вычислим величину полного перемещения сечения С по формуле:
и изобразив эпюру перемещений системы (рис. 1, з), вычислим величину полного перемещения сечения С по формуле:
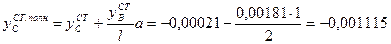 м.
м.
2. Определение динамического коэффициента и коэффициента эквивалентности. Максимальное значение системы внешних сил принимает значение 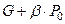 . Далее определяем коэффициент эквивалентности:
. Далее определяем коэффициент эквивалентности:
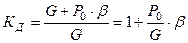 ,
,
где 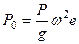 - амплитудное значение инерционной силы;
- амплитудное значение инерционной силы; 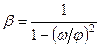 - коэффициент динамичности. Здесь
- коэффициент динамичности. Здесь 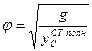 -частота собственных колебаний;
-частота собственных колебаний; 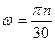 - частота возмущающей силы.
- частота возмущающей силы.
В рассматриваемом примере:
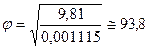
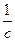 ;
; 
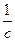 ;
;
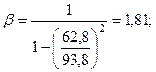
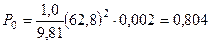 кН;
кН;
 .
.
3. Определение прогиба и напряжений. Максимальное значение напряжения и прогиб, возникающие от совместного действия статических и динамических нагрузок, определяем по формулам:
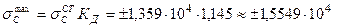 кН/м2,
кН/м2,
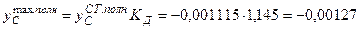 м.
м.
При коэффициенте КД = 1, 145 найдем также напряжение в сечении А балки АВ:
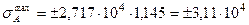 кН/м2.
кН/м2.
Следовательно, полученное значение напряжения больше, чем напряжение в сечении С, где установлен электромотор. Итак, сечение в заделке в данном примере является наиболее опасным  , и, следовательно, это обстоятельство необходимо учитывать при проверке прочности составных конструкций.
, и, следовательно, это обстоятельство необходимо учитывать при проверке прочности составных конструкций.
С увеличением числа оборотов двигателя возрастают динамические напряжения и прогибы балок. Поэтому при проектировании конструкций не следует допускать наступления резонанса (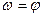 ), при котором может наступить разрушение конструкции.
), при котором может наступить разрушение конструкции.