Пример 29.

Определить частоты собственных колебаний балки с двумя сосредоточенными массами (рис. 1).

а) б)

Рис. 1

Решение.

Для определения частот собственных колебаний имеем уравнение

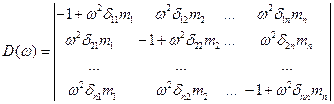, которое для n = 2 принимает вид:

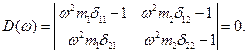(1)

Раскрывая определитель (1), получим:

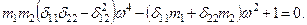(2)

На рис. 2 построены эпюры моментов от единичных сил:

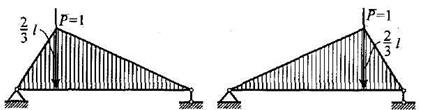
а) б)

Рис. 2

Согласно формуле Мора 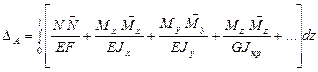имеем:

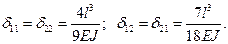
Если принять 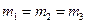, то из (2) получим:

причем 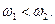Таким образом, система имеет две собственные частоты колебаний,

Полагая в 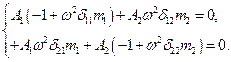, получим . Полагая 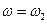найдем 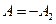. В первом случае массы колеблются в одной фазе (рис. 1, а), во втором случае - в противо-фазе (рис.1, б).

В общем случае колебания с частотам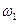и и 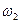происходят одновременно. Закон движения в этом случае (каждой массы) будет:

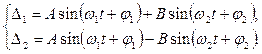(3)

где А, В, 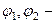постоянные, определяемые из начальных условий.

Пример 30.

Определить критическое число n оборотов мотора, вес которого 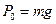(рис. 1, а).

Решение.

При критическом числе оборотов мотора имеет место резонанс, условием которого будет:

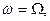
где

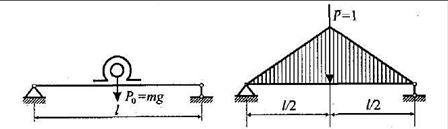
а) б)

Рис. 1

На основании формулы Мора и рис. 1, б, находим:

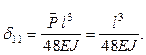
Следовательно,