
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи на смеси и сплавы
⇐ ПредыдущаяСтр 11 из 11
|
|
Задачи этого раздела вызывают наибольшие затруднения. Очень важно разобраться в самом тексте задачи. Необходимо научиться расчленять такую задачу на ряд простейших.
Задачи, в которых отношение компонентов смеси задано в процентах
Пример 21.
В14. Имеются два сосуда, содержащие 42 кг и 6 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 40% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 50% кислоты. Сколько кг кислоты содержится в первом растворе?
Решение:
Масса смеси равна 42 + 6 = 48 кг.
Пусть х кг кислоты содержится в 42 кг первого раствора,
у кг кислоты содержится в 6 кг второго раствора,
тогда 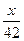 кг кислоты содержится в 1 кг первого раствора, кг кислоты содержится в 1 кг первого раствора,
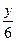 кг кислоты содержится в 1 кг второго раствора, кг кислоты содержится в 1 кг второго раствора,
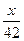 · 24 = · 24 = 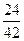 х кг кислоты содержится в 24 кг первого раствора, х кг кислоты содержится в 24 кг первого раствора,
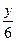 · 24 = · 24 = 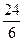 у кг кислоты содержится в 24 кг второго раствора.
В 40%-ной смеси содержится 48 · 0, 4 = 19, 2 кг кислоты, т.е. х + у = 19, 2.
В 50%-ной смеси содержится 48 · 0, 5 = 24 кг кислоты, т.е. у кг кислоты содержится в 24 кг второго раствора.
В 40%-ной смеси содержится 48 · 0, 4 = 19, 2 кг кислоты, т.е. х + у = 19, 2.
В 50%-ной смеси содержится 48 · 0, 5 = 24 кг кислоты, т.е. 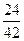 х + х + 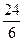 у = 24.
Составим систему и решим ее: у = 24.
Составим систему и решим ее: 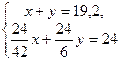 Умножим обе части второго уравнения на Умножим обе части второго уравнения на 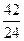 , получим: , получим: 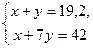 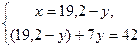 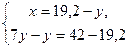
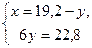 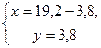 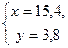 Значит, 15, 4 кг кислоты содержится в первом растворе.
В бланк ответов: 15, 4
Значит, 15, 4 кг кислоты содержится в первом растворе.
В бланк ответов: 15, 4
|