
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Работа № 1.4.
|
|
Математическое описание объекта с использованием плана эксперимента второго порядка
Планы эксперимента второго порядка обеспечивают получение уравнения регрессии, включающего линейные эффекты, парные взаимодействия и квадратичные эффекты, т.е. уравнения следующего вида
Ù
|
|
b 0 -свободный член уравнения регрессии;
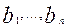 -коэффициенты регрессии, отражающие эффекты первого порядка;
-коэффициенты регрессии, отражающие эффекты первого порядка;
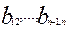 |
|
Из планов второго порядка рассмотрим центральные композиционные планы.
В основе центрального композиционного плана лежит полный факторный план первого порядка или полуреплика от него. Кроме того добавляются опыты в центре эксперимента и в звездных точках.
Согласно рис. 1.4.1. для числа факторов n =2 в двумерном факторном пространстве опытные точки ПФП расположены в вершинах квадрата. Координаты этих точек соответствуют уровням факторов в нормализованном масштабе т.е. А (+1, +1), В (-1, +1), С (-1, -1), Д (+1, -1). Центр эксперимента 0 имеет координаты (0, 0), а звездные точки расположены на расстоянии звездного плеча а от центра эксперимента и имеют координаты К (+ а, 0), М (- а, 0), L (0, + а), Т (0, - а).
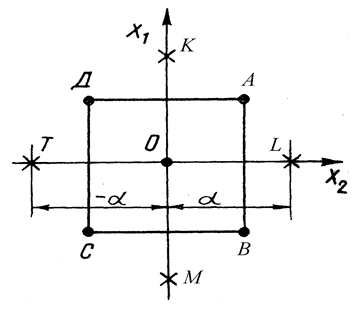
Рис. 1.4.1
Аналогичным образом строятся центральные композиционные планы для другого числа факторов. Ортогональный план эксперимента второго порядка для трех факторов в нормализованном масштабе представлен в таблице 1.4.1.
Таблица 1.4.1.
| № опыта | Уровни факторов | № опыта | Уровни факторов | ||||
| x1 | x2 | x3 | X1 | x2 | x3 | ||
| +1 | +1 | +1 | +а | ||||
| -1 | +1 | -1 | -а | ||||
| +1 | -1 | -1 | +а | ||||
| -1 | -1 | +1 | -а | ||||
| +1 | +1 | -1 | |||||
| -1 | +1 | +1 | |||||
| +1 | -1 | +1 | |||||
| -1 | -1 | -1 | |||||
| +а | |||||||
| -а |
В таблице 1.4.2 приведены параметры ортогональных центральных композиционных планов эксперимента для числа входных факторов n=2-4.
Таблица 1.4.2.
| Число факторов | Параметры плана | ||
| Ядро (основа) плана | Величина звёздного плеча | Число опытов в центре | |
| ПФП Nя=4 | a=1.00 | N0=1 | |
| ПФП Nя=8 | a=1.215 | N0=1 | |
| ПФП Nя=16 | a=1.414 | N0=1 |
Для центрального композиционного планирования переход от натурального масштаба факторов к нормализованному и наоборот производится на основании соотношений (1.2.1) – (1.2.4), однако интервал варьирования здесь равен
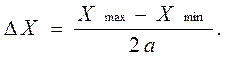
(1.4.2)
В случаях, когда уравнение регрессии, полученное по плану экспе-римента первого порядка оказалось неадекватным, переходят к плану эксперимента второго порядка. Тогда опыты плана эксперимента первого порядка можно сохранить и дополнить прежний план опытами в звездных и центральной точках.. При этом расширяются диапазоны варьирования факторов. Новые границы диапазонов факторов 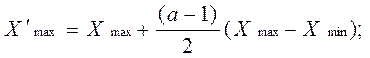 Х¢ max и X¢ min будут равны:
Х¢ max и X¢ min будут равны:
(1.4.3)
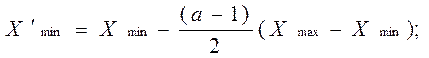
Порядок работы.
1. Задать (рассчитать) диапазоны варьирования факторов X¢ 1min, X¢ 1max, X¢ 2min, X¢ 2max, X¢ 3min, X¢ 3max и т.д. .
2. Построить центральный композиционный план эксперимента для n =3 согласно табл. 1.4.1 в нормализованномм и натуральном масштабе факторов, используя формулы перехода (1.2.4), (1.4.2).
3. Выполнить пробный опыт в центре эксперимента с числом измерений 50-100. По ним рассчитать дисперсию воспроизводимости s 2y по формуле (1.1.3), предварительно отбросив грубые измерения (см. Работу 1.1)
4. Определить число измерений k во всех остальных опытах по формуле (1.2.7).
5. Выполнить все опыты, получив в каждом ряд измерений. Вычислить для каждого u -го опыта среднюю арифметическую ` Yu и среднее квадратическое отклонение sy по формулам (1.1.2) и (1.1.4). Записать данные по форме таблицы 1.4.3. Если отбрасываются грубые измерения, то объём выборки для каждого опыта следует дополнить новыми измерениями (см. пункт 5 Работы 1.2).
Таблица 1.4.3.
| № п/п | x0 | x1 | x2 | x3 | x1 x2 | x1x3 | x2 x3 | x12 | x22 | x32 | `Yu | su |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | |||
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | +1 | +1 | |||
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | |||
| . | . | . | . | . | . | . | . | . | . | . | ||
| . | . | . | . | . | . | . | . | . | . | . | ||
| +1 | +а | а2 | ||||||||||
| . | . | . | . | . | . | . | . | . | . | . | ||
| . | . | . | . | . | . | . | . | . | . | . | ||
| +1 |
6. Проверить гипотезу об однородности дисперсий (см. пункт 6 работы № 1.3.).
7. Вычислить коэффициенты регрессии по формулам регрессионного анализа в матричной форме.
Расчеты выполняют с использованием таблицы 1.4.2. Записать уравнение регрессии согласно формуле (1.4.1).
8. Далее производится статистический анализ полученного уравнения регрессии.
Сначала проверяют гипотезу о значимости коэффициентов регрессии. Рассчитываем значения t-критерия Стьюдента по формуле (1.2.5). Следует указать, что при этом для планов второго порядка, в котором ошибки коэффициентов регрессии различны для разных эффектов, значения t-критерия будет несколько завышенным. Тогда для некоторых незначимых эффектов повышается вероятность их признания доминирующими.
Критические значения t-критерия определяются по таблице 1.2.6 (см. Работу 1.2).
9. Проверить статистическую гипотезу об адекватности полученного упрощенного уравнения регрессии по F-критерию Фишера (см. пункт 10 Работы 1.3).
10. Записать упрощенное уравнение регрессии и перевести его в натуральный масштаб факторов (форм.1.2.1, 1.4.2)
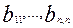 - -коэффициенты регрессии, отражающие эффекты второго порядка (квадратичные эффекты).
эффекты второго порядка (квадратичн
ые эффекты).
- -коэффициенты регрессии, отражающие эффекты второго порядка (квадратичные эффекты).
эффекты второго порядка (квадратичн
ые эффекты).