Решение типовых задач. Определение математического ожидания, дисперсии,

Тема №1.

Определение математического ожидания, дисперсии,

Корреляционной функции

Теоретические сведения

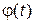Пусть – неслучайная функция, 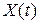, 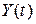– независимые случайные функции.

Свойства математического ожидания:

1)

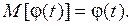
2)

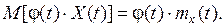
3)

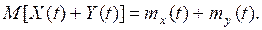
4)

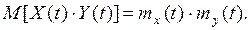
Пусть 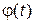– неслучайная функция, 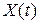, 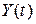– независимые случайные функции, тогда дисперсия случайно величины :

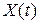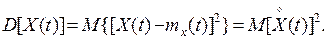
Свойства дисперсии:

1)

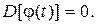
2)

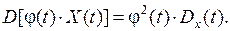
3)

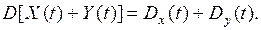
4)

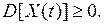
Пусть 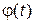– неслучайная функция, 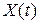– случайная функция.

Корреляционной функцией называется математическое ожидание произведения значений случайной функции 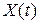для двух моментов времени :

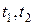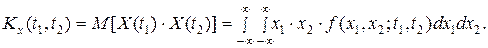
Свойства корреляционной функции:

1.

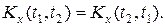
Для стационарных процессов 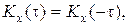где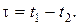

2.

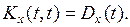
3. Пусть 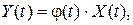тогда

4. Пусть 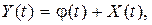тогда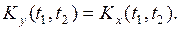

5. Пусть 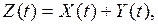тогда

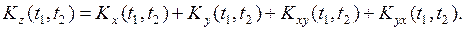
6. Пусть 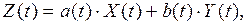где 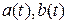– неслучайные, тогда

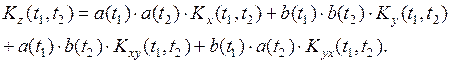
Решение типовых задач

Пример 1.1. Определить математическое ожидание произведения двух функций 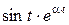, где

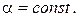
Решение. Используем первое свойство математического ожидания, так как обе функции неслучайные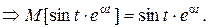

Пример 1.2. Определить математическое ожидания следующего выражения 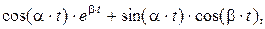где

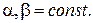
Решение. Сначала используем третье свойство математического ожидания:

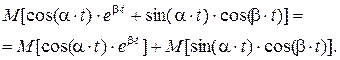
Затем применим первое свойство математического ожидания

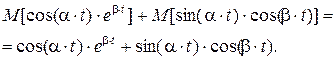
Пример 1.3. Определить дисперсию следующего выражения:

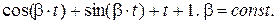
Решение. Используем первое свойство дисперсии, так как все четыре слагаемых данного выражения неслучайные функции:

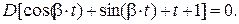
Пример 1.4. Определить корреляционную функцию .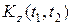

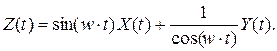
Решение. Используем сначала пятое, затем третье свойства корреляционной функции:

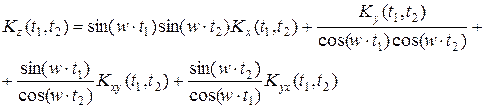
Пример 1.5. Определить корреляционную функцию .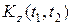

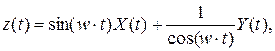если 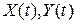– независимые.

Решение. Используем третье свойство корреляционной функции: