
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. Учебно-методическое пособие
|
|
В. А. Шкель
ВЫСШАЯ
МАТЕМАТИКА
Случайные величины
Учебно-методическое пособие
Минск 2007
УДК 51(076.1)
ББК 22.11
Ш 66
Рекомендовано к изданию редакционно-издательским советом
Частного института управления и предпринимательства
А в т о р
доцент кафедры высшей математики и статистики
Частного института управления и предпринимательства
кандидат физико-математических наук, старший научный сотрудник
В. А. Шкель
Р е ц е н з е н т ы:
главный научный сотрудник Института математики
НАН Беларуси доктор физико-математических наук В. А. Цурко;
доцент кафедры высшей математики
Белорусского государственного экономического университета
кандидат физико-математических наук, доцент Н. В. Денисенко
Рассмотрено и одобрено
на заседании кафедры высшей математики и статистики,
протокол № 3 от 04.10.2006 г.
|
Высшая математика. Случайные величины: учеб.-метод. пособие / В. А. Шкель.– Минск: Частн. ин-т упр. и предпр., 2007.– 56 с.
В пособии рассматриваются вероятностные функции для дискретных и непрерывных случайных величин, некоторые законы распределения, даются определения числовых характеристик.
Предназначено для студентов дневной и заочной форм обучения Частного института управления и предпринимательства.
УДК 51(076.1)
ББК 22.11
© Шкель В. А., 2007.
Лекция 1. Виды случайных величин.
Функции распределения вероятностей случайных величин
План
1. Виды случайных величин. Закон распределения вероятностей дискретной случайной величины.
2. Функция распределения вероятностей случайной величины.
3. Плотность распределения вероятностей непрерывной случайной величины.
Ключевые слова
Случайная величина. Дискретная случайная величина. Непрерывная случайная величина. Закон распределения случайной величины. Ряд и полигон распределения. Функция распределения случайной величины. Плотность распределения вероятностей
1. Виды случайных величин. Закон распределения
вероятностей дискретной случайной величины
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Пример 1.1. Число родившихся мальчиков среди 10 новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, …, 10.
Пример 1.2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины лежат в некотором промежутке (а, b).
Будем обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами х, y, z. Например, если случайная величина Х имеет три возможных значения, то они будут обозначены х 1, х 2, х 3.
Вернемся к примерам, приведенным выше. В первом из них случайная величина Х могла принять одно из следующих возможных значений: 0, 1, 2, …, 10. Эти значения отделены друг от друга промежутками, в которых нет возможных значений Х, т. е. в этом примере случайная величина принимает отдельные, изолированные возможные значения. Во втором примере случайная величина могла принять любое из значений промежутка (а, b). Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины.
Уже из сказанного можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счетным). Множество, состоящее из бесконечного числа элементов, которые могут быть перенумерованы натуральными числами, называется счетным.
Непрерывной называют случайную величину, которая может принимать все возможные значения из некоторого конечного или бесконечного промежутка. Очевидно, что число возможных значений непрерывной случайной величины бесконечно. Примеры непрерывной случайной величины: рост, вес, возраст случайно встреченного человека, доход на одного человека в месяц, дневная выручка магазина и др.
Для описания дискретной случайной величины необходимо указать не только множество ее возможных значений, но и вероятности, с которыми принимаются те или иные значения. Такое описание случайной величины называется ее законом распределения.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически. Если обозначить возможные числовые значения случайной величины Х через х 1, х 2, …, хп, а через 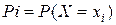 – вероятность появления значения хі, то дискретная случайная величина полностью определяется таблицей
– вероятность появления значения хі, то дискретная случайная величина полностью определяется таблицей
| Хі | х 1, х 2... хп |
| Рі | р 1, р 2... рп |
Здесь значения х 1, х 2,..., хп записываются, как правило, в порядке возрастания. Таблица называется рядом распределения дискретной случайной величины Х. Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события 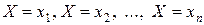 образуют полную группу, следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:
образуют полную группу, следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:
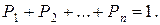
Если множество возможных значений Х бесконечно (счетно), то ряд 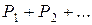 сходится и его сумма равна единице.
сходится и его сумма равна единице.
Пример 1.3. В лотерее разыгрываются 100 билетов, среди которых один выигрыш в 40 у.е., 5 выигрышей по 20 у.е., 10 выигрышей по 10 у.е. и 15 – по 5 у.е. Составить ряд распределения случайной величины Х – суммы выигрыша на один билет.
Случайная величина Х может принимать значения 0, 5, 10, 20, 40, тогда ряд распределения будет иметь вид:
| хі | 0 5 10 20 40 |
| рі | 0, 69 0, 15 0, 10 0, 05 0, 01 |
Контроль: 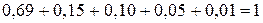 .
.
Для наглядности ряд распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки  а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником или полигоном распределения.
а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником или полигоном распределения.
Пример 1.4. Построить полигон распределения случайной величины Х примера 1.3.
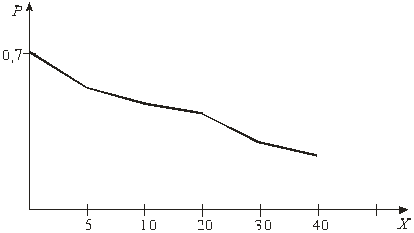
Рис. 1.1
Пример 1.5. В коробке 7 карандашей, из которых 4 красные. Из этой коробки наугад извлекаются 3 карандаша. Найти закон (ряд) распределения случайной величины Х, равной числу красных карандашей в выборке.
В выборке из трех карандашей может не оказаться ни одного красного карандаша, может появиться один, два или три карандаша. Следовательно, случайная величина Х может принимать только четыре значения: 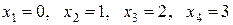 . Вычислим вероятности этих значений:
. Вычислим вероятности этих значений:
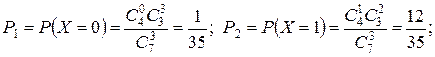

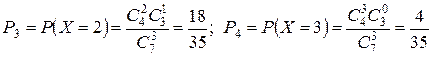 .
.
Следовательно, случайная величина Х имеет ряд распределения
| хі | 0 1 2 3 |
| рі | 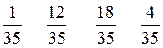
|
Отметим, что 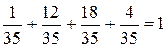 .
.
Пример 1.6. Дискретная случайная величина Х имеет закон распределения
| хі | 3 4 5 6 7 |
| рі | р 1 0, 15 р 3 0, 25 0, 35 |
Найти вероятность 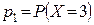 и
и 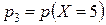 , если известно, что р 3 в 4 раза больше р 1.
, если известно, что р 3 в 4 раза больше р 1.
Так как 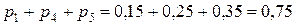 , то
, то 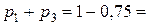 = 0, 25. Поскольку
= 0, 25. Поскольку 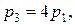 то
то 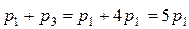 , значит,
, значит, 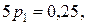 откуда
откуда 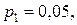 следовательно,
следовательно, 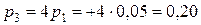 . Итак:
. Итак: 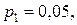
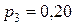 .
.
Две случайные величины Х и Y называются независимыми, если события 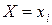 и
и 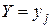 независимы для всех значений
независимы для всех значений 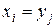 . Это означает, что
. Это означает, что 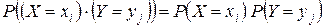 .
.
Пусть случайные величины Х и Y имеют ряды распределения соответственно:
| хі | х 1 х 2... хп | уj | y1 y 2 … ym | |
| рі | р 1 р 2... рп | qj | q 1 q 2 … qm |
Введем новые случайные величины. Величина 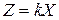 , где k – постоянная величина, есть также случайная величина, которая принимает значение kxі с теми же самыми вероятностями, что и случайная величина Х, принимающая значения хі, т. е.
, где k – постоянная величина, есть также случайная величина, которая принимает значение kxі с теми же самыми вероятностями, что и случайная величина Х, принимающая значения хі, т. е. 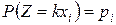 . Ряд распределения случайной величины Z может быть записан в виде таблицы
. Ряд распределения случайной величины Z может быть записан в виде таблицы
| Zі | kx 1 kx 2 … kxn |
| Pі | р 1 p 2 … pn |
Квадрат случайной величины 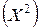 – это новая случайная величина, которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные квадратам ее значений.
– это новая случайная величина, которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные квадратам ее значений.
Сумма случайных величин Х и Y – это новая случайная величина 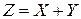 , принимающая все значения вида
, принимающая все значения вида 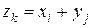 с вероятностями
с вероятностями
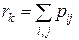 при
при 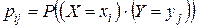 .
.
Суммирование производится по тем значениям индексов і и j, для которых 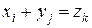 . Если при этом случайные величины Х и Y независимы, то
. Если при этом случайные величины Х и Y независимы, то
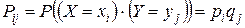 .
.
Разностью случайных величин называется новая случайная величина 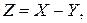 для которой
для которой
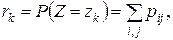 где
где 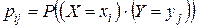 ,
, 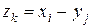 .
.
Пример 1.7. Случайные величины Х и Y независимы и заданы рядами распределения
| xi | 0 1 2 3 | yj | –1 0 1 | |
| pi | 0, 2 0, 4 0, 3 0, 1 | qj | 0, 4 0, 2 0, 4 |
Найти закон распределения случайной величины 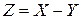 .
.
Все возможные значения разности случайных величин 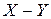 составляют множество чисел
составляют множество чисел 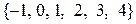 . Определим их вероятности:
. Определим их вероятности:
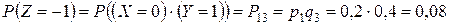 ;
;
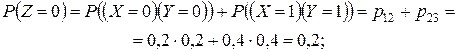
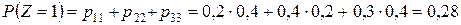 ;
;
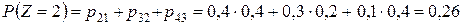 ;
;
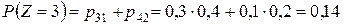 ;
;
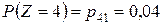 .
.
Итак, ряд распределения случайной величины Z имеет вид
| zk | –1 0 1 2 3 4 |
| rk | 0, 06 0, 20 0, 28 0, 26 0, 14 0, 04 |
Произведением случайных величин Х и Y называется новая случайная величина 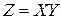 , принимающая все значения вида
, принимающая все значения вида 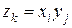 с вероятностями
с вероятностями
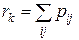 , где
, где  .
.
Здесь суммирование производится по тем значениям индексов i и j, для которых 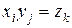 .
.
Вопросы для самопроверки
1.Что называется случайной величиной?
2. Какую величину называют дискретной случайной величиной?
3. Какую величину называют непрерывной случайной величиной?
4. Что называют законом распределения дискретной случайной величины?
5. Как задают закон распределения дискретной случайной величины?
6. Что называют многоугольником распределения?
7. Как задают закон распределения дискретной случайной величины, принимающей счетное множество значений?
8. Какое условие определяет независимость случайных величин?
9. Какие арифметические операции можно производить над случайными величинами?
Упражнения
1. Задают ли законы распределения дискретной случайной величины следующие таблицы?
| а) | хi | 2 3 4 5 | б) | хi | 6 7 8 9 | |
| pi | 0, 1 0, 4 0, 3 0, 2 | pi | 0, 1 0, 2 0, 3 0, 5 |
| в) | хi | 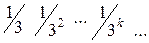
| г) | хi | 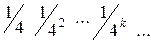
| |
| pi | 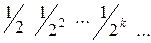
| pi | 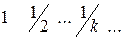
|
2. Дискретная случайная величина Х имеет ряд распределения
| хi | 0, 2 0, 4 0, 6 0, 8 1 |
| pi | 0, 1 0, 2 0, 4 р 4 0, 1 |
Чему равна вероятность 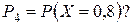 Построить многоугольник распределения.
Построить многоугольник распределения.
3. Подбрасываются два игральных кубика и подсчитывается число очков, выпавших на обеих верхних гранях. Найти закон распределения дискретной случайной величины Х – суммы выпавших очков на двух игральных кубиках.
4. Составить закон распределения вероятностей числа появлений события А в трех независимых испытаниях, если вероятность появления события в каждом испытании равна 0, 6.
5. На пути движения автомашины 4 светофора. Каждый из них либо разрешает, либо запрещает дальнейшее движение автомашины с вероятностью 0, 5. Построить полигон распределения.
6. Два студента сдают 2 зачета. Вероятность того, что первый студент сдаст любой из зачетов равна 0, 9, а второй – 0, 8. Составить закон распределения и построить полигон общего числа сданных зачетов.
7. При некотором технологическом процессе брак составляет в среднем 3%. Составить закон распределения числа стандартных изделий среди взятых наудачу 4 изделий этого производства.
8. Даны независимые случайные величины Х и Y
| хі | 1 2 3 | уj | –2 –1 0 | |
| рі | 0, 1 0, 3 0, 6 | qj | 0, 6 0, 3 0, 1 |
Записать закон распределения суммы 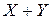 и произведения ХY случайных величин Х и Y.
и произведения ХY случайных величин Х и Y.
9. В городе 10 коммерческих банков. У каждого риск банкротства в течение года составляет 10%. Составить ряд распределения числа банков, которые могут обанкротиться в течение следующего года.
10. Подбрасываются три игральных кубика и подсчитывается число очков на верхних гранях кубиков. Найти закон распределения дискретной случайной величины, равной сумме очков, выпавших на трех кубиках.
11. Отдел рекламы фирмы поместил свою рекламу в 10 из 25 городских газет. Покупатель приобрел 3 различные газеты. Составить закон распределения числа газет, приобретенных покупателем, в которых размещена реклама фирмы.
12. Записи страховой компании показали, что 30% держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. Для проверки в случайном порядке было отобрано 15 человек старше 50 лет, имеющих полисы. Составить ряд распределения числа предъявленных претензий.
13. В магазине имеется 15 автомобилей определенной марки. Среди них – 7 черного цвета, 6 – серого и 2 – белого. Представители фирмы обратились в магазин с предложением о продаже им трех автомобилей этой марки, безразлично какого цвета. Составить ряд распределения числа проданных автомобилей черного цвета при условии, что автомобили отбирались случайно, и построить его график.
14. Телевизионный канал рекламирует новый вид детского питания. Вероятность того, что телезритель увидит эту рекламу, оценивается в 0, 2. В случайном порядке выбраны 10 телезрителей. Составить ряд распределения числа лиц, видевших рекламу.