
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случайной величины
|
|
Дискретная случайная величина может быть задана перечнем всех ее возможных значений и их вероятностей. Такой способ задания не является общим: он не применим, например, для непрерывных случайных величин.
Действительно, рассмотрим случайную величину Х, возможные значения которой сплошь заполняют интервал (а, b). Очевидно, что нельзя составить перечень всех возможных значений Х. Этот пример указывает на целесообразность дать общий способ задания любых типов случайных величин. С этой целью и вводят функции распределения вероятностей случайной величины.
Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т. е. вероятность события 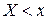 , обозначим
, обозначим 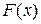 . Разумеется, если х изменяется, то, вообще говоря, изменяется и
. Разумеется, если х изменяется, то, вообще говоря, изменяется и 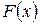 , т. е.
, т. е. 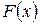 – функция от х.
– функция от х.
Функцией распределения называют функцию 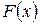 , определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т. е.
, определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т. е. 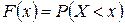 .
.
Геометрически это равенство можно истолковать так: 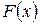 есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Иногда вместо термина «функция распределения» используют термины «интегральная функция» или «интегральный закон распределения». Теперь можно дать более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Функция распределения 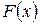 случайной вели ч ины Х имеет следующие свойства:
случайной вели ч ины Х имеет следующие свойства:
1. Все значения функции распределения 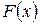 принадлежат отрезку [0, 1], т. е.
принадлежат отрезку [0, 1], т. е. 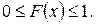
Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.
2. 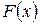 – неубывающая функция, т. е.
– неубывающая функция, т. е. 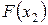 ≥
≥ 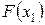 , если
, если 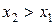 .
.
Из этого свойства вытекают два важных следствия:
а) вероятность того, что случайная величина примет значение, заключенное в интервале [ a, b), равна приращению функции распределения на этом интервале:
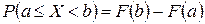 .
.
Пример 2.1. Случайная величина Х задана функцией распределения:
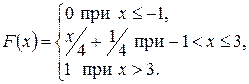
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0, 2):
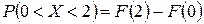 .
.
Так как на интервале (0, 2) по условию 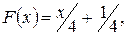
то
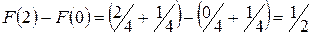 .
.
Итак: 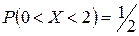 ;
;
б) вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.
Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Этот факт полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером.
Заметим, что было бы неправильным думать, что равенство нулю вероятности 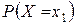 означает, что событие
означает, что событие 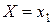 невозможно (если, конечно, не ограничиваться классическим определением вероятности). Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений, в частности, это значение может оказаться равным х 1.
невозможно (если, конечно, не ограничиваться классическим определением вероятности). Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений, в частности, это значение может оказаться равным х 1.
3. Если возможные значения случайной величины принадлежат интервалу 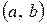 , то
, то  при
при  ,
, 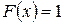 при
при 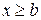 .
.
С л е д с т в и е. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:
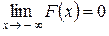 ;
; 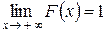 .
.
4. Функция 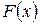 в точке х 0 непрерывна слева, т. е.
в точке х 0 непрерывна слева, т. е.
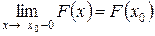 .
.
Функция распределения 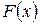 для дискретной случайной величины Х, которая может принимать значения х 1, х 2, … хп с соответствующими вероятностями, имеет вид
для дискретной случайной величины Х, которая может принимать значения х 1, х 2, … хп с соответствующими вероятностями, имеет вид
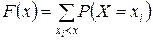 ,
,
где символ 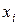 < х означает, что суммируются вероятности тех значений, которые меньше х. В данном случае функция является разрывной (имеет ступенчатый вид). Приведенные свойства позволяют представить, как выглядит график функции распределения.
< х означает, что суммируются вероятности тех значений, которые меньше х. В данном случае функция является разрывной (имеет ступенчатый вид). Приведенные свойства позволяют представить, как выглядит график функции распределения.
Для дискретных случайных величин функция распределения 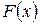 есть разрывная ступенчатая функция, непрерывная слева (рис. 2.1):
есть разрывная ступенчатая функция, непрерывная слева (рис. 2.1):
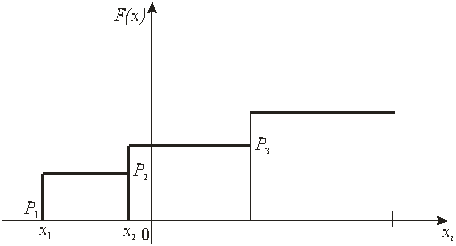
Рис. 2.1
График расположен в полосе, ограниченной прямыми 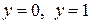 . При возрастании х в интервале
. При возрастании х в интервале 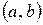 , в котором заключены все возможные значения случайной величины, график «поднимается вверх». При
, в котором заключены все возможные значения случайной величины, график «поднимается вверх». При  ординаты графика равны нулю, при
ординаты графика равны нулю, при 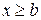 ординаты графика равны единице.
ординаты графика равны единице.
Пример 2.2. Дана функция
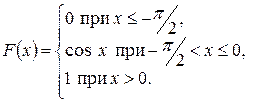
Показать, что эта функция является функцией распределения некоторой случайной величины Х.
График функции 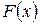 имеет вид:
имеет вид:
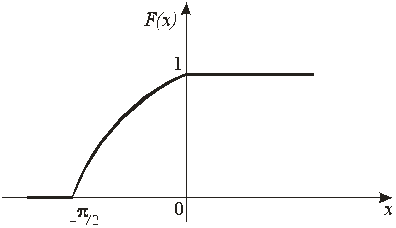
Рис. 2.2
Все значения этой величины принадлежат отрезку 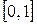 , так как
, так как  Функция
Функция 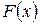 является неубывающей: в промежутке
является неубывающей: в промежутке 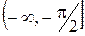 она постоянная, равна нулю, в промежутке
она постоянная, равна нулю, в промежутке  возрастает, в промежутке
возрастает, в промежутке 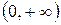 также постоянная, равная единице. Функция непрерывна в каждой точке х 0 области ее определения – промежутка
также постоянная, равная единице. Функция непрерывна в каждой точке х 0 области ее определения – промежутка 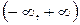 , поэтому непрерывна слева и справа.
, поэтому непрерывна слева и справа.
Следовательно, функция 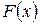 удовлетворяет всем свойствам, характерным для функции распределения. Функция
удовлетворяет всем свойствам, характерным для функции распределения. Функция 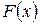 является функцией распределения некоторой случайной величины Х.
является функцией распределения некоторой случайной величины Х.
Пример 2.3. Дискретная случайная величина Х задана рядом распределения
| хi | 1 4 8 |
| рi | 0, 3 0, 1 0, 6 |
Найти функцию распределения и вычертить ее график.
Если 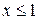 , то
, то  (третье свойство). Если
(третье свойство). Если 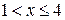 , то
, то 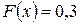 . Действительно, Х может принять значение 1 с вероятностью 0, 3. Если
. Действительно, Х может принять значение 1 с вероятностью 0, 3. Если 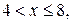 то
то 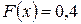 . Действительно, если х 1 удовлетворяет неравенству
. Действительно, если х 1 удовлетворяет неравенству 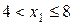 , то
, то 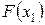 равна вероятности события
равна вероятности события 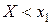 , которое может быть осуществлено, когда Х примет значение 1 (вероятность этого события равна 0, 3) или значение 1 (вероятность этого события равна 0, 1). Поскольку эти два события несовместны, то по теореме сложения вероятность события
, которое может быть осуществлено, когда Х примет значение 1 (вероятность этого события равна 0, 3) или значение 1 (вероятность этого события равна 0, 1). Поскольку эти два события несовместны, то по теореме сложения вероятность события 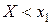 равна сумме вероятностей
равна сумме вероятностей  . Если
. Если 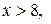 то
то 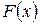 =1. Действительно, событие
=1. Действительно, событие 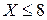 достоверно, следовательно, его вероятность равна единице.
достоверно, следовательно, его вероятность равна единице.
Итак, функция распределения аналитически может быть записана так:
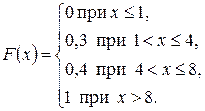
График этой функции приведен на рис. 2.3.
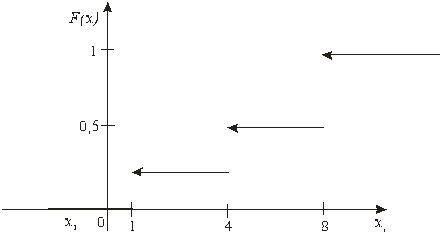
Рис. 2.3
Вопросы для самопроверки
1. Как определяется функция распределения случайной величины?
2. Какие другие названия используют для функции распределения?
3. Как с помощью функции распределения вычислить вероятность того, что случайная величина примет значение из полуинтервала 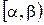 ?
?
4. Какую случайную величину называют непрерывной?
5. Какими свойствами обладает функция распределения?
6. Какой вид имеет график функции распределения?
7. Чему равна вероятность того, что непрерывная случайная величина примет одно, заданное определенное значение?
8. Можно ли утверждать, что событие А является невозможным, если 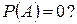
9. Как определяется функция распределения для дискретной случайной величины?
10. Является ли непрерывной функция распределения для дискретной случайной величины?
11. Чему равны наименьшее и наибольшее значения функции распределения?
12. Что определяет величина скачка функции распределения дискретной случайной величины?