Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 1. Закон распределения дискретной случайной величины задан таблицей
|
|
1. Закон распределения дискретной случайной величины задан таблицей
| хi | 3 6 9 12 |
| рi | 0, 1 0, 2 0, 3 0, 4 |
Найти математическое ожидание случайных величин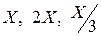 
.
2. Случайная величина задана плотностью распределения:
а)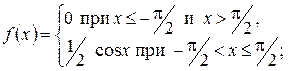 
б)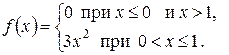 
Найти математическое ожидание.
3. Случайная величина Х задана функцией распределения:
а)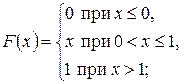 
б) 
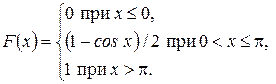
Найти математическое ожидание случайной величины Х.
4. Найти математическое ожидание случайной величины: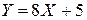 
, если известно, что 
.
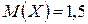5. Известны математические ожидания двух случайных величин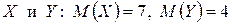 
. Найти математическое ожидание суммы и разности этих величин.
6. Известны математические ожидания двух независимых случайных величин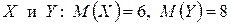 
. Найти математическое ожидание их произведения.
7. Охотник, имеющий 4 патрона, стреляет в цель до первого попадания (или пока не израсходует все патроны). Найти математическое ожидание числа израсходованных патронов, если вероятность попадания при каждом выстреле равна 0, 25.
8. Рабочий обслуживает 4 станка. Вероятность того, что в течение часа не потребуется внимания рабочего для первого станка, равна 0, 9, для второго – 0, 8, для третьего – 0, 75 и для четвертого – 0, 7. Найти математическое ожидание числа станков, которые не потребуют внимания рабочего в течение часа.
2. Дисперсия случайной величины.
Среднее квадратическое отклонение
Рассмотрим случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения. Пусть дискретные случайные величины Х и Y заданы следующими законами распределения
| Х | – 0, 01 0, 01 | Y | – 100 100 | |
| Р | 0, 5 0, 5 | Р | 0, 5 0, 5 |
Найдем математические ожидания этих величин:
;
.
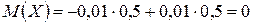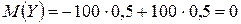Итак, математическое ожидание обеих величин одинаково, а возможные значения различны, причем Х имеет значения, близкие к математическому ожиданию, а Y – далекие от своего математического ожидания. Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание не характеризует полностью случайную величину. В связи с этим наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
На первый взгляд, может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины (разность между случайной величиной и ее математическим ожиданием) и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е.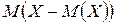 
, как нетрудно показать, любой случайной величины равно нулю. Это объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны,
в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Правда,
в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
Дисперсией, или рассеянием, случайной величины называют мате-матическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
.
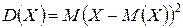Дисперсия дискретной случайной величины с законом распределения
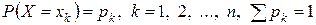
определяется формулой
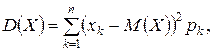
или формулой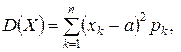 
где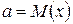 
– другое обозначение для математического обеспечения.
Если дискретная случайная величина принимает бесконечную последовательность значений с законом распределения
,
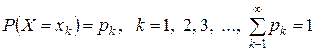то ее дисперсия определяется формулой
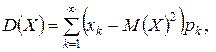
при условии, что этот ряд сходится.
Дисперсия непрерывной случайной величины Х, все значения которой принадлежат отрезку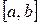 
, определяется формулой
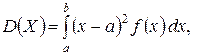
где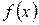 
– плотность распределения вероятностей этой величины, 
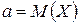– ее математическое ожидание.
Дисперсия непрерывной случайной величины Х, все значения которой принадлежат промежутку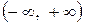 
, определяется формулой
если этот несобственный интеграл сходится абсолютно.
Из определения следует, что дисперсия случайной величины есть неслучайная (постоянная) величина.
Пример 2.1. Найти дисперсию случайной величины Х, которая задана законом распределения
| Х | 1 2 5 |
| Р | 0, 3 0, 5 0, 2 |
Найдем математическое ожидание
.
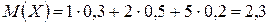Значения квадрата отклонения
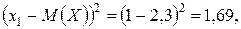
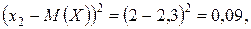
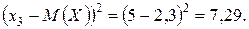
По определению дисперсии
.
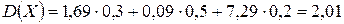Пример 2.2. Найти дисперсию случайной величины Х, заданной плотностью распределения
,
.
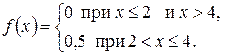
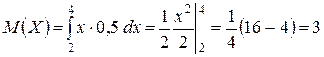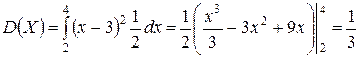Для вычисления дисперсии часто бывает удобно пользоваться формулой
,
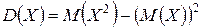т. е. дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.
Пример 2.3. Найти дисперсию случайной величины Х, которая задана законом распределения
| Х | 2 3 5 |
| Р | 0, 1 0, 6 0, 3 |
.
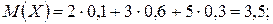
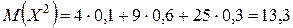Искомая дисперсия
.
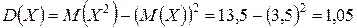Казалось бы, если Х и Y имеют одинаковые возможные значения и одно и то же математическое ожидание, то и дисперсии этих величин равны (ведь возможные значения обеих величин одинаково рассеяны вокруг своих математических ожиданий). Однако в общем случае это не так. Дело в том, что одинаковые возможные значения рассматриваемых величин имеют, вообще говоря, различные вероятности, а величина дисперсии определяется не только самими возможными значениями, но и их вероятностями. Например, если вероятности «далеких» от математического ожидания возможных значений Х больше, чем вероятности этих же значений Y,
и вероятности «близких» значений Х меньше, чем вероятности тех же значений Y, то, очевидно, дисперсия Х больше дисперсии Y.
Пример 2.4. Сравнить дисперсии случайных величин, заданных законами распределения
| Х | – 1 1 2 3 | Y | – 1 1 2 3 | |
| Р | 0, 48 0, 01 0, 09 0, 42 | Р | 0, 19 0, 51 0, 25 0, 05 |
; 
.
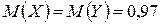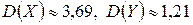Возможные значения и математические ожидания Х и Y одинаковы, а дисперсии различны, причем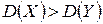 
. Этот результат можно было предвидеть без вычислений, глядя лишь на законы распределения.