
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моменты случайных величин
|
|
Рассмотрим дискретную случайную величину Х, заданную законом распределения
| Х | 1 2 5 100 |
| Р | 0, 6 0, 2 0, 19 0, 01 |
Найдем математическое ожидание Х:
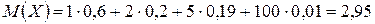 .
.
Найдем математическое ожидание случайной величины Х 2:
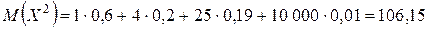 .
.
Видим, что 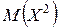 значительно больше
значительно больше 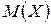 . Это объясняется тем, что после возведения в квадрат возможное значение величины Х 2, соответствующее значению
. Это объясняется тем, что после возведения в квадрат возможное значение величины Х 2, соответствующее значению 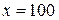 величины Х, стало равным 10 000, т. е. значительно увеличилось; вероятность же этого значения мала – 0, 01.
величины Х, стало равным 10 000, т. е. значительно увеличилось; вероятность же этого значения мала – 0, 01.
Таким образом, переход от 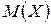 к
к 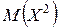 позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина Х имела несколько больших и маловероятных значений, то переход к величине Х 2, а тем более к величинам
позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина Х имела несколько больших и маловероятных значений, то переход к величине Х 2, а тем более к величинам 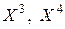 и т. д., позволил бы еще больше усилить роль этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).
и т. д., позволил бы еще больше усилить роль этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).
Начальным моментом vk порядка k случайной величины Х назы-вается математическое ожидание k-ой ее степени:
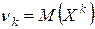 .
.
Если дискретная случайная величина принимает конечное множество значений, то по определению
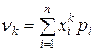 .
.
Если дискретная случайная величина принимает счетное множество значений, то
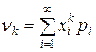 ,
,
когда этот ряд сходится абсолютно. (В этой и предыдущей формуле 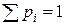 ).
).
Начальный момент порядка k непрерывной случайной величины с плотностью распределения 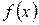 определяется формулой
определяется формулой
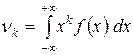 ,
,
если интеграл сходится абсолютно.
Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения этой величины от ее математического ожидания. Обозначив центральный момент k -го порядка через m k и положив 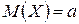 , по определению получим:
, по определению получим:
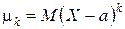 .
.
Для дискретной случайной величины
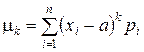 или
или 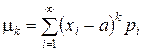 .
.
Для непрерывной случайной величины с плотностью распределения 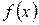 центральный момент k -го порядка определяется по формуле
центральный момент k -го порядка определяется по формуле
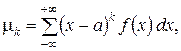
если интеграл сходится абсолютно.
Легко выводятся соотношения, связывающие начальные и центральные моменты:
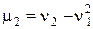 ,
,
 ,
,
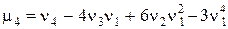 .
.
Моменты более высоких порядков применяются редко.
Пример 3.1. Дискретная случайная величина задана законом распределения
| Х | 1 2 |
| Р | 0, 4 0, 6 |
Найти центральные моменты первого, второго и третьего порядков.
Находим сначала начальные моменты:
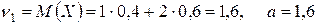
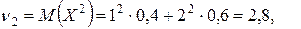
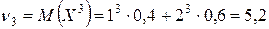 ,
,
тогда
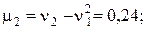
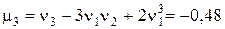 .
.
Пример 3.2. Найти начальный момент второго порядка случайной величины с плотностью вероятностей
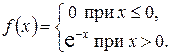
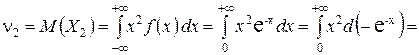
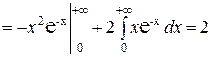 .
.
Нетрудно показать, что начальный момент нулевого порядка равен единице, начальный момент первого порядка равен ее математическому ожиданию, центральные моменты нулевого, первого и второго порядка равны соответственно единице, нулю и дисперсии.
Вопросы для самопроверки
1. Что называют начальным моментом k -го порядка случайной величины?
2. По какой формуле вычисляются начальные моменты k -го порядка случайной величины, принимающей конечное множество значений?
3. Какой формулой определяется начальный момент k -го порядка случайной величины, принимающей счетное множество значений?
4. Какой формулой определяется начальный момент k -го порядка непрерывной случайной величины?
5. Что называется центральным моментом k -го порядка случайной величины?
6. По какой формуле вычисляется центральный момент k -го порядка случайной величины, принимающей конечное множество значений?
7. Какой формулой определяется центральный момент k -го порядка случайной величины, принимающей счетное множество значений?
8. Какой формулой определяется центральный момент k -го порядка непрерывной случайной величины?
9. Чему равны начальные моменты нулевого порядка, первого порядка?
10. Чему равны центральные моменты нулевого, первого, второго порядков?
11. Как выражаются центральные моменты второго порядка через начальные моменты?
12. Как выражаются центральные моменты третьего порядка через начальные моменты?