Биномиальное распределение

Пусть в одинаковых условиях производится п независимых испытаний, в результате каждого из которых может появиться событие А с вероятностью р. В каждой серии из п испытаний событие А может либо не появиться, либо появиться 1 раз, 2 раза, …, п раз. Рассмотрим дискретную случайную величину Х – число появлений события А при п испытаниях. Величина Х может принимать значение 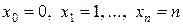. Вероятность 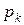того, что случайная величина Х принимает значение 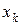, вычисляется по формуле Бернулли.

Закон распределения дискретной случайной величины, определяемый формулой Бернулли, называется биномиальным. Постоянные п и р, входящие в формулу Бернулли, называются параметрами биномиального распределения.

Биномиальный закон распределения дискретной случайной величины можно представить в виде следующей таблицы:

Х			… k	… n
Р	qn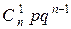

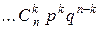
Можно показать, что для случайной величины Х, распределенной по биномиальному закону, математическое ожидание равно произведению параметров 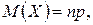дисперсия равна произведению npq, .

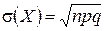Пример 4.2.1. Проверкой качества установлено, что из каждых 100 деталей не имеют дефектов 75 штук в среднем. Составить биномиальное распределение вероятностей числа пригодных деталей из взятых наугад 6 деталей.

Из условия задачи следует, что .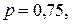

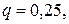
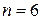По формуле Бернулли

,

,

, ,

.

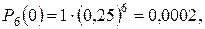
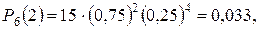
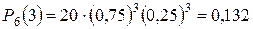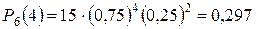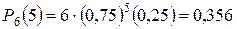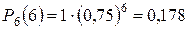Закон распределения имеет вид

Вопросы для самопроверки

1. Какое распределение вероятностей называется биномиальным?

2. Чем объясняется слово «биномиальный» в названии распределения?

3. Чему равно математическое ожидание случайной величины, распределенной по биномиальному закону, с параметрами п и р?

4. Чему равна дисперсия случайной величины, распределенной по биномиальному закону, с параметрами п и р?

5. Чему равно среднее квадратическое отклонение случайной величины, распределенной по биномиальному закону, с параметрами п и р?

6. Запишите биномиальный закон распределения вероятностной случайной величины в виде таблицы.