Распределение Пуассона

В одинаковых условиях производится п независимых испытаний, в каждом из которых может появиться событие А с вероятностью р или событие Ā с вероятностью 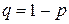. Вероятность того, что при п испытаниях событие Ā появится k раз (и не появится п-k раз), определяется формулой Бернулли. Рассмотрим случай, когда п являются достаточно большим, а р – достаточно малым. Положим 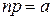, где а – некоторое число.

Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой

.

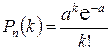Постоянную а = пр называют параметром распределения Пуассона.

Распределение Пуассона является предельным случаем биномиаль-ного распределения, т. е.

.

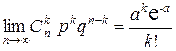Можно показать, что математическое ожидание и дисперсия дискретной случайной величины, распределенной по закону Пуассона, равны числу а – параметру этого распределения.

Иногда полезно использовать рекуррентную формулу

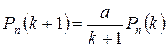, которая получается следующим образом:

.

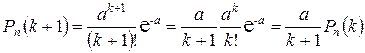Пример 4.3.1. Вероятность изготовления нестандартной детали 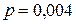. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных.

Здесь ,

тогда .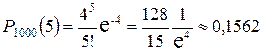

Пример 4.3.2. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 минуты равна 0, 002. Найти вероятность того, что в течение 1 минуты обрыв произойдет более чем на трех веретенах.

В соответствии с условиями:

.

;

.

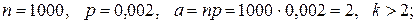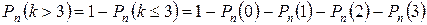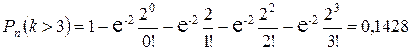Вопросы для самопроверки

1. Почему закон распределения Пуассона называется законом редких событий?

2. При каких условиях можно применять закон распределения Пуассона?

3. Что является случайной величиной в законе Пуассона?

4. Каковы общие условия, необходимые для применимости закона распределения Пуассона и закона биномиального распределения?

5. Как связаны между собой биномиальное распределение и распределение Пуассона?

6. Чему равны математические ожидания и дисперсия случайной величины, распределенной по закону Пуассона?

7. Какая из величин в законе Пуассона больше: математическое ожидание или число независимых испытаний?

8. Исследуется распределение Пуассона. Что вероятнее: событие А появится ровно один раз или ни разу?