Равномерное распределение. Распределение вероятностей случайной величины Х называется равномерным на отрезке [a, b], если плотность вероятностей этой величины постоянна на данном

Распределение вероятностей случайной величины Х называется равномерным на отрезке [a, b], если плотность вероятностей этой величины постоянна на данном отрезке и равна нулю вне этого отрезка:

С равномерным распределением встречаются всякий раз, когда по условиям опыта величина Х принимает значение в конечном промежутке 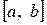. Все значения из этого промежутка возможны в одинаковой степени, причем ни одно из значений не имеет преимущество перед другими. Вот примеры такого рода: 1) Х – время ожидания на стоянке автобуса (величина Х равномерно распределена на отрезке 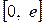, где е – интервал движения между автобусами); 2) Х – ошибка при взвешивании случайно выбранного предмета, получающаяся от округления результата взвешивания до ближайшего целого числа (величина Х имеет равномерное распределение на отрезке 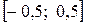, где за единицу принята цена деления шкалы).

Нетрудно показать, что для равномерно распределенной на отрезке 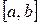случайной величины Х функции плотности вероятностей и функция распределения имеют вид:

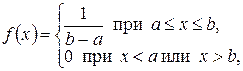
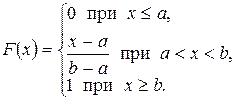
Вероятность попадания значений случайной величины Х в интервал 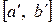, принадлежащий отрезку 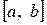, определяется равенством

.

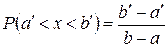Математическое ожидание и дисперсия случайной величины соответственно равны

, .

Пример 4.4.1. Случайная величина Х равномерно распределена на отрезке 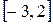. Записать плотность распределения 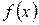, функцию распределения 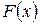этой случайной величины, найти математическое ожидание и дисперсию.

В нашем случае 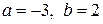и значит

, .

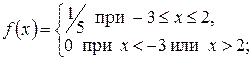
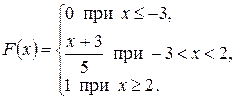
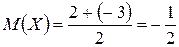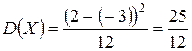Вопросы для самопроверки

1. Какое распределение вероятностей называется равномерным на отрезке [ a, b ]?

2. Как записать плотность распределения f(x) случайной величины Х, равномерно распределенной на отрезке [ a, b ]?

3. Какой вид имеет функция распределения F (x) случайной величины, равномерно распределенной на отрезке [ a, b ]?

4. Чему равно математическое ожидание случайной величины, равномерно распределенной на отрезке [ a, b ]?

5. Чему равна дисперсия случайной величины Х, равномерно распределенной на отрезке [ a, b ]?

6. Чему равно среднее квадратическое отклонение случайной величины Х, равномерно распределенной на отрезке [ a, b ]?

7. Случайная величина Х равномерно распределена на отрезке [ a, b ]. Как найти вероятность попадания ее значений в интервал 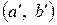, принадлежащий данному отрезку?